Planimetria uwu: W czworokącie ABCD punkty K,L,M,N są środkami boków odpowiednio AB,BC,CD,DA. W punktach X,Y,Z,T przecinają się pary odcinków, odpowiednio: AM i BN, BN i CK, CK i DL, DL i AK. Wykaż że: [XYZT]= [AXN] + [BYK] + [CZL] + [DTM] oraz że [AKYX] + [CMTZ] = [BLZY] + [DNXT] Ma ktoś jakieś pomysły?

PW: Nie. Nie wiem co miałby oznaczać symbol [XYZT] dla czwórki punktów, a co [BYK] dla trójki punktów.

jc: Pole czworokąta / trójkąta?

ite: Pewnie tak jak tutaj https://www.mimuw.edu.pl/~joasiaj/plock/materialy/pola_trojkatow_zadan.pdf : Nawias kwadratowy oznacza pole figury.

ite:

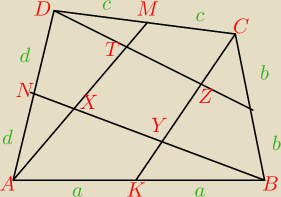
uwu: Z tego co wnioskuje patrząc na treść to rysunek może wyglądać tak, ale nie jestem pewien czy wszystko się zgadza

uwu: Jednak już jestem pewien że wszystko się zgadza

PW: @ite, jestem pełen podziwu dla ilustracji byka. Normalnie Lascaux.

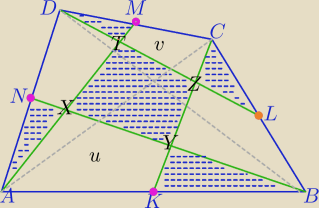
Mila: CK−środkowa w ΔABC AM− środkowa w ΔACD⇔ [ADM]=[ACM] i [AKC]=[BKC]

	1		1		1
[AKC]+[ACM]=		[ABC]+		[CDA]=		[ABCD]⇔
	2		2		2

	1
[AKC]+[ACM]=[AKCM]=		[ABCD]
	2

Analogicznie wykazujemy, że:

	1
[BLD]+[BND]=[LCD]+[ABN]=		[ABCD]⇔
	2

[AKCM]=[LCD]+[ABN] /−(u+v) Ozn. [AKYX]=u, [TZCM]=v [AKCM]=[LCD]+[ABN] L=[AKMC]−u−v=[XYZT] P=([LCD]−v)+([ABN]−u)=[ZLC]+[MTD]+[AXN]+[BKY] ⇔ [XYZT]=[ZLC]+[MTD]+[AXN]+[BKY] ============================ cnd Drugą równość spróbuj sam.

uwu: Dzięki za pomoc b zrobiłbym tak:

	1		1
KBC + CAD =		ABCD ⇔ AKCM =		ABCD
	2		2

	1		1
ABN + LCD =		ABCD ⇔ NBLD =		ABCD
	2		2

AKCM = NBLD AKCM = AKYX + XYZT + TZCM NBLD = NXTD + XYZT + YBLZ AKYX + XYZT + TZCM = NXTD + XYZT + YBLZ | −XYZT AKYX + TZCM = NXTD + YBLZ cnw PS. czy kolejność liter którymi opisuje figurę ma znaczenie? przykładowo jeśli mam kwadrat o wierzchołkach ABCD to czy nazwanie go kwadratem DABC albo ACDB będzie błędem?

uwu: zrobiłem błąd w pierwszym równianiu.

	1		1
Powinno być : KBC + MAD =		ABCD ⇔ AKCM =		ABCD
	2		2

uwu: Czy to zadanie da się zrobić w podobny sposób? W równoległoboku ABCD kąt przy wierzchołku A jest ostry. Punkty E, F, G, H są środkami boków odpowiednio AB, BC, CD oraz DA. Punkty przecięcia prostych: AF i DE, AF i BG, CH i GB oraz CH i DE są wierzchołkami czworokąta KLMN.

	KLMN		1
Wykaż, że:		=
	ABCD		5

.

Mila: (b) Krócej: Korzystając z (1) [AKCM]=[DNLB] [AKYX]+ [XYZT]+ [CMTZ]=[BLYZ]+ [XYZT]+[DNTX]⇔ [AKYX] + [CMTZ] = [BLZY] + [DNXT] cnw ========================

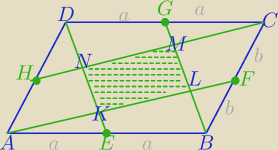
Mila: Podpowiedź: 1) [ABCD]=P

	1		1		1
[AED]+[GBC]=		P+		P=		P
	4		4		2

	1
[EBGD]=		P=[AFCH]
	2

2) Skorzystaj z podobieństwa Δ △CMG∼ΔCDN⇔[CDN]=4*[CMG] Dalej sam, w razie kłopotów pisz .

6latek: Przepraszam bardzo ale ja dalej nie wiem co oznacza np [ABCD] Autor wali glupa i nie napisal Przepraszam ale to jest tak samo jakbym np zapytala czy ciag {x_n}(zbiezny do zera ) to x_n=o(1) Prawda to czy nieprawda ? Pierwsze pytanie ktore powinno padnac to co to jest =0(1) ? Dobrej nocy wszystkim. Kolorowych snow

Mila: Zapis [ABC] oznacza pole trójkąta

Mila: Trójkąta ABC

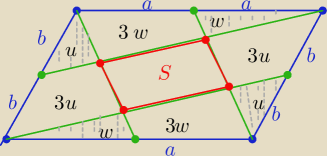
Eta: u+w+w+u=S (jak poprzednio) 2w+2u=S P=8w+8u+S P=4S+S

S		1
	=
P		5

uwu: Czemu [CMG] : [CND] = 4 : 1 skoro [CG] : [CD] = 2 : 1

Mila:

	|CG|		1
△CMG∼ΔCDN w skali k=		=
	|CD|		2

stosunek pól figur podobnych jest równy kwadratowi skali podobiństwa⇔

[CMG]		1
	=		⇔
[CDN]		4

[CDN]=4*[CMG] Popatrz na rozwiązanie Ety, masz to wykorzystane.

uwu: już rozumiem dzięki wielkie