trudne hubik: Trójkąt ABC jest rozwartokątny o kącie rozwartym przy wierzchołku C a kąt przy wierzchołku A ma miarę dwa razy większą od miary kąta przy wierzchołku B Przez wierzchołek B poprowadzono prostą prostopadłą do boku BC przecinającą przedłużenie boku AC w punkcie D, ponad to punkt S jest środkiem boku AB Wykaż,ze miary katów AMC i BMD są równe Mógłby ktoś pomóc ? bardzo byłbym wdzięczny

wredulus_pospolitus: A czym że jest ów tajemniczy punkt M

mat: Myślę,że zamiast M napisał S ( ale tylko tak myślę

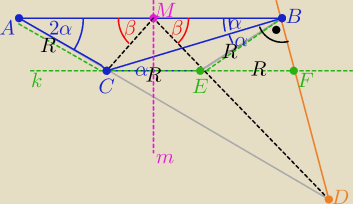
Eta: Patrząc na rysunek ..... Dodaj hubik odpowiednie dokładne komentarze uwzględniając: 1/ΔCFB prostokątny , E −− środek okręgu opisany na nim⇒ ΔCEB równoramienny⇒ ..... 2/Czworokąt ACEB −− jest trapezem równoramiennym o dolnej podstawie i ramionach długości R 3/ prosta m jest symetralną ΔCEM ⇒ teza : kąty β mają równe miary Skąd masz to zadanie ? z jakiegoś konkursu?