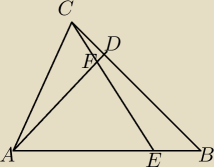
 Pole trójkąta ABC jest równe 273. Na bokach AB i BC tego trójkąta ABC wybrano takie
punkty odpowiednio E i D, że AE : EB = BD : DC = 5:2. Odcinki AD i CE przecinają się w
punkcie F
Oblicz: [AEF], [CDF], [AFC], [BDFE].
Odpowiedzi to: b) [AEF]=125, [BEFD]= [AFC]=70, [CDF]=8, jednak nie wiem skąd one się biorą.
Próbowałem układać różne proporcje i układy ale nie mogę wyznaczyć tych pól.
Pole trójkąta ABC jest równe 273. Na bokach AB i BC tego trójkąta ABC wybrano takie
punkty odpowiednio E i D, że AE : EB = BD : DC = 5:2. Odcinki AD i CE przecinają się w
punkcie F
Oblicz: [AEF], [CDF], [AFC], [BDFE].
Odpowiedzi to: b) [AEF]=125, [BEFD]= [AFC]=70, [CDF]=8, jednak nie wiem skąd one się biorą.
Próbowałem układać różne proporcje i układy ale nie mogę wyznaczyć tych pól.
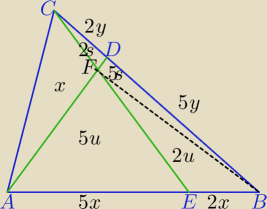 [ABC]=273
[ABC]=273
| 5 | ||
[AEC]= | *273=5*39=195=[ABD] | |
| 7 |
| 2 | ||
[CEB]= | *273=2*39=78 | |
| 7 |
| [AEC] | 5 | ||
= | − Δ mają tę samą wysokość | ||
| [CEB] | 2 |