Prawda/fałsz z uzasadnieniem Dejsza: Problem mam z rozumieniem tego typu zadań https://imgur.com/a/Ofx1Nd7

wredulus_pospolitus: 1) skoro funkcja jest różniczkowalna w puncie 'a' to funkcja f(x) MUSI być ciągła w tymże punkcie 'a' (innymi słowy −−− ciągłość funkcji w przedziale (a,b) jest warunkiem KONIECZNYM na różniczkowalność funkcji na przedziale (a,b) ) f'(a) = 0 jest warunkiem koniecznym, ale NIE WYSTARCZAJĄCYM aby funkcja f(x) posiadała ekstremum w punkcie x = a Przykład: f(x) = x³ ... f'(x) = 2x² .... jak widzisz f'(0) = 0, ale w tym punkcie (x=0) funkcja nie posiada ekstremum, tylko punkt przegięcia a trzecia odpowiedź jest w ogóle bez sensu (czyli oczywiście: NIE)

wredulus_pospolitus: 2) Wiemy, że jest różniczkowalna w x = 1 ; nie wiemy czy jest różniczkowalna w każdym innym punkcie czy też ciągła Patrz to co wcześniej napisałem (odnośnie ekstremum) Tak ... funkcja MOŻE (ale nie musi) mieć w x=1 ekstremum (patrz co wcześniej napisałem)

wredulus_pospolitus: 3) Nie musi być malejąca NA CAŁYM przedziale (0 ; 1) −−− może na przykład najpierw trochę rosnąć i dopiero później zacząć maleć To w ogóle jest bez sensu −−− może nie mieć ani jednego rozwiązania to równanie ( f(x) = 4 ) Tak ... na mocy tw. Derboux wiemy, że ciągła funkcja f(x) przyjmuje każdą wartość z przedziału (−2 ; 2) ... więc także przyjmie wartość równą 0

wredulus_pospolitus: 4) spróbuj samodzielnie (jest podobne do (3) )

wredulus_pospolitus: 5) f(x) = e^|x| rozpatrujemy sytuację dla x<0 ... wtedy możemy zapisać: f(x) = e^|x| = e^−x więc f'(x) = − e^−x = − e^|x|

wredulus_pospolitus: spójrz na wykres g(x) = e^x spójrz na wykres h(x) = e^−x Twoja funkcja f(x) = e^|x| będzie 'częściowo' miała postać jednej z funkcji (dla x≥0) a częściowo drugiej (dla x<0) Czy któraś z tych funkcji przyjmuje chociażby wartość równą −1? W takim razie czy funkcja f(x) ma nieograniczony zbiór wartości (czyli jest nieograniczona)

π		3.14		0.14
	≈		= 1 +		> 1
3		3		3

i teraz spójrz na wykresy g(x) i h(x) i zastanów się nad odpowiedzią

wredulus_pospolitus: 6) spróbuj samodzielnie

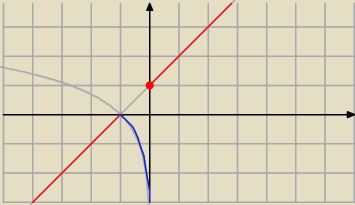
wredulus_pospolitus: 7) najlepiej NARYSUJ wykres tej funkcji A zauważysz łatwo czy jest to surjekcja z R na R Czy są punkty nieciągłości I czy f(x) = a ma dwa rozwiązania dla a<0

wredulus_pospolitus: 8) spróbuj samodzielnie (też zacznij od narysowania tejże funkcji)

Dejsza: Tylko jak mam rozumieć surjekcję? W wykładach mam napisane jedynie to: Funkcja f: X→Y jest surjekcją wtedy i tylko wtedy, gdy f(X)=Y, czyli gdy przeciwdziedzina funkcji f jest jej zbiorem wartości. Nie wiem, jak mam to czytać z wykresu.

wredulus_pospolitus: surjekcja 'na chłopski rozum' jest wtedy gdy: funkcja przyjmuje KAŻDĄ wartość ze zbioru Y przynajmniej raz czyli: f: R −> [0;+∞) ; f(x) = x² JEST surjekcją f: R −> R ; f(x) = x² NIE JEST surjekcją (bo funkcja nie przyjmuje wartości chociażby −1)

Dejsza: A co w przypadku, jak mamy taką sytuację jak na 7?

Dejsza: Jest surjekcją tylko dla x+1 z wyłączeniem x∊(−1;0)?

wredulus_pospolitus: W (7) funkcja f(x) to to czerwona i niebieska krzywa (szara już nie) W takim razie łatwo zauważyć 'przerwę' na przedziale y ∊ (0;1) ... innymi słowy ... f(x) =

	1
		(na przykład) NIE MA rozwiązań
	2

związku z tym ...

Dejsza: Ah, więc o takie coś chodzi. Po prostu patrzysz na wartości na y, czy nie ma jakichś przerw.

wredulus_pospolitus: nie tyle czy nie ma 'jakiś przerw' co czy przeciwdziedzina funkcji zawiera cały zbiór Y (dany w zadaniu) W tym konkretnym zadaniu zbiór Y = R ... dlatego szukasz (jakiejkolwiek) przerwy " na y'rekach "

Dejsza: Zadanie 7. Wyjaśnisz mi, jak się sprawdzało punkty nieciągłości?

Jerzy: Funkcja jest ciagła w punkcie, gdy: 1) Posiada wartość w tym punkcie 2) Posiada granicę w tym punkcie 3) Granica jest równa wartości funkcji

Dejsza: A jak jest w przypadku funkcji z zadania 7? Żebym miała podgląd na to, jak rozwiązać?

Jerzy: Które punkty twoim zdaniem są podejrzane ? Czy funkcja posiada wartość w tych punktach ?

Dejsza: Moim zdaniem punkt x = 0 jest podejrzany. Dla ln(−x) nie znamy wartości, zaś dla x+1 mamy wartość.

Jerzy: Funkcja nie jest ciągła w punkcie x = 0 , bo nie posiada granicy w tym punkcie. Granica lewostronna to − ∞ , a granica prawostronna to 1. W punkcie x = − 1 funkcja jest ciagła.

Dejsza: Teoretycznie posiada granicę, ale tylko jednostronną.

Jerzy: Co to znaczy "teoretycznie posiada granicę" ?

Adamm: Czyli granicy nie posiada

Jerzy: Funkcja posiada granicę w punkcie, gdy lewostronna jest równa prawostronnej. Ta funkcja posiada granicę w punkcie x = −1 , ale nie posiada granicy w punkcie x = 0

Dejsza: Miałabym też pytanie odnośnie: Każda funkcja, która jest ograniczona, jest też ciągła − raczej to jest prawda na mocy Weierstrassa, tak?

Dejsza: Rozumiem, czyli sprawdzać z obu stron granicę.

Adamm: Funkcja ciągła na odcinku domkniętym jest ograniczona. Funkcja ograniczona jest ciągła? No nie. Wystarczy prosty przykład f(x) = 0 dla x≠0, f(0) = 1

Adamm: Ogólnie, funkcja ciągła f:X→R (dla pewności X − przestrzeń Hausdorffa ) jest ograniczona jeśli X jest zwarty.

Dejsza: O przestrzeni Hausdorffa nie miałam.

Adamm: Spokojnie. Nie musisz wiedzieć. Pewnie nie będziesz.

Dejsza: W sumie samo twierdzenie Weierstrassa starczy, bo tam jest o zbiorze domkniętym i ograniczonym.