ASYMPTOTA MONOTONICZNOŚĆ Student: 1.Dana jest funkcja Tornqvista f trzeciego rodzaju (dobra luksusowe) f(x)=3x(x−2) / x+1 , x≥2 (a) Wyznaczyć asymptotę ukośną funkcji f (b) Zbadać monotoniczność funkcji f w przedziale (2,+∞) 2.Opisać metodę badania ekstremów lokalnych funkcji rzeczywistych jednej zmiennej i zbadać istnienie oraz rodzaj ekstremów lokalnych funkcji f(x)=2x³+3x²−12x+6 Czy f posiada punkty przegięcia? 3.Obliczyć całkę oznaczoną ∫¹ a na dole −2 (x+2)(1−x)dx i podać interpretacje geometryczną uzyskanego wyniku 4.Zbadać istnienie oraz rodzaj ekstremów lokalnych funkcji : f(x,y) = −x²−5y²+4xy−2x+6y−2 BARDZO POTRZEBUJE ROZWIĄZANIA TYCH ZADAŃ Z OBLICZENIAMI NA JUŻ

Adamm: BARDZO POTRZEBUJE ROZWIĄZANIA TYCH ZADAŃ Z OBLICZENIAMI NA JUŻemotka no i za to większość ludzi by cię już kompletnie skreśliło polecam zapoznać się z tym jak pisać pytania, z większym szacunkiem

Student: Bardzo potrzebuję ponieważ jutro muszę to oddać a dowiedziałem się niedawno o tym a aktualnie jestem w pracy. Przepraszam jeśli kogokolwiek uraziłem. Czekam skromnie z niecierpliwością aby może ktoś wspomógł.

Adamm: Też się naucz pisać ułamki, chociaż nawiasy powstawiaj 3x(x−2) / x+1 i 3x(x−2) / (x+1) to nie jest to samo

	3x(x−2)		3x(x−2)
pierwsze oznacza		+1 a drugie
	x		x+1

Student: Przepraszam w takim razie jest tak jak piszesz. 3x(x−2) / (x+1) to jest poprawne. Piszę z telefonu w pracy dlatego pośpiech wyszedł. Dziękuję za poprawę.

wredulus_pospolitus: To się 'rychło w czas' obudziłeś. A jaką wiedzę z zajęć wyniosłeś? Maturę jakoś zdałeś, więc pierwsze i drugie zadanie powinieneś być w stanie zrobić nawet bez wiedzy 'ze studiów'.

wredulus_pospolitus: 1 a) asymptota ukośna:

	f(x)		U{3x(x−2}
I) liczysz granicę limx−>+∞		= limx−> +∞		{x} = ... i
	x		x+1)

otrzymana wartość to Twoje 'a' II) liczysz granicę lim_{x−> +∞} f(x) − a*x ... gdzie 'a' to te 'a' ze wcześniejszej granicy ... a wynik tej granicy to Twoje 'b' asymptota ukośna będzie miała wzór: y(x) = a*x + b ; gdzie a i b to wartości wyliczonych granic Analogicznie robisz dla x−> −∞ Uwaga: Jeżeli pierwsza z granic wyjdzie +∞ lub −∞ to asymptota ukośna NIE ISTNIEJE.

Student: Niestety byłem pewien ostatni czas za granicą z powodów zdrowotnych. Aktualnie jestem w pracy do 6 rano. Wsiadam w auto i jadę prosto na uczelnie. Nie mam po prostu czasu ani nawet kartki czy długopisu aby rozwiązać te zadania w pracy. Bardzo proszę o pomoc.

wredulus_pospolitus: 1 b) monotoniczność funkcji I) wyznaczasz dziedzinę funkcji II) liczysz pochodną funkcji (czyli f'(x) ) III) sprawdzasz kiedy pochodna funkcji jest większa od zera, a kiedy mniejsza czyli rozwiązujesz: f'(x) > 0 oraz f'(x) < 0 IV) gdy f'(x) > 0 to funkcja f(x) jest w tym przedziale rosnąca ... analogicznie gdy f'(x) < 0 to w tym przedziale funkcja f(x) jest malejąca

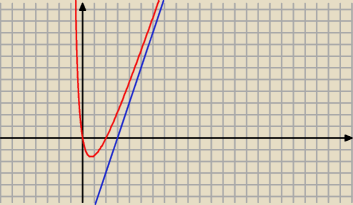
Adamm: 1. Asymptota ukośna to taka funkcja liniowa y = ax+b, że lim_x→∞ (f(x)−ax−b) = 0 lub lim_x→−∞ (f(x)−ax−b) = 0 w pierwszym przypadku mówimy o asymptocie prawostronnej, w drugiej o lewostronnej obliczamy w ten sposób

	f(x)
a = limx→±∞		, b = limx→±∞ (f(x)−ax)
	x

tu możemy mieć jedynie asymptotę prawostronną a = 3, b = −9 monotoniczność sprawdzamy przez obliczenie pochodnej i sprawdzenie jej znaku

	3(x2+2x−2)
f'(x) =		> 0 dla x≥2
	(x+1)2

wredulus_pospolitus: Tyle podam od siebie. Z całym szacunkiem − chcę Ci wierzyć, zwłaszcza że nie masz postawy 'roszczeniowej', ale jednak z całym szacunkiem ... nie będę podawał Ci gotowca na parę godzin przed terminem oddania. Rozumiem, że różne sytuacje mogą się przydarzyć i każdy czasem staje pod ścianą. Natomiast zadania te to jest de facto podsumowanie semestru/roku z analizy matematycznej i powinieneś potrafić je rozwiązać (przynajmniej część z nich wiedzieć jak zrobić). Nie wiem gdzie pracujesz, ale skoro masz 'nockę' to zapewne masz możliwość zagospodarowania sobie 'chwili czasu' na zrobienie tych zadań. A skoro od razu jedziesz na uczelnię, to chyba jakiś długopis i zeszyt (jakąś kartkę) powinieneś mieć w samochodzie.

Student: Dobra dzięki bardzo.

Adamm: 4. f(x,y) = −x²−5y²+4xy−2x+6y−2 warunek konieczny f_x = 0, f_y = 0 f_x(x, y) = −2x+4y−2 f_y(x, y) = −10y+4x+6 rozwiązujemy układ, dostajemy x = 1, y = 1 to jedyny punkt który może być ekstremalny teraz sprawdzamy macierz Hessego f_xx f_xy f_yx f_yy f_xx = −2, f_yy = −10, f_xy = f_yx = 4 (tu mamy https://pl.wikipedia.org/wiki/Twierdzenie_Schwarza) wyznacznik macierzy Hessego = (−2)*(−10)−4*4 = 4 > 0 f_xx(1, 1) < 0 więc w tym punkcie mamy maksimum lokalne gdyby było f_xx > 0 to byłoby minimum, a gdyby Hesjan < 0 to nie byłoby ekstremum.

Adamm: 2/4 powinno wystarczyć

Student: Dziękuje bardzo!