jest / nie jest różniczkowalna w kazek: Niech f : R→R, f(x) = |x−2|.Wówczas funkcja f: jest / nie jest różniczkowalna w x0 = 2, bo

Adamm: Nie ufam ludziom co zmieniają co chwilę nicki.

kazek: Ok, dzięki za pomoc

kazek:

	⎧	x−2 gdy x≥2
f(x) =|x−2| =	⎩	−x+2 gdy x<2

f(x₀)=f(2)=0

	f(x0+h)−f(x0)
f`(x0)=limh−>2
	h

	h−0
limh−>2+		=1
	h

	−h−0
himh−>2−		=−1
	h

Czy to dobrze ?

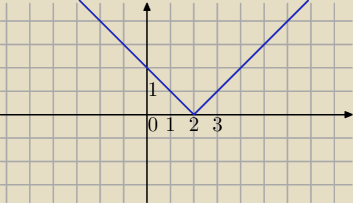
Mila: Dobrze. Popatrz na wykres. W x=2 na wykresie masz "szpic".

Adamm: Tak zazwyczaj wyglądają funkcje lipszycowsko ciągłe. Tutaj mamy |f(x)−f(y)| ≤ |x−y|, f jest lipszycowska ze stałą 1

kazek: To już totalnie teraz nie rozumiem

kazek:

	|x−2|−|2−2|		|x−2|
limx−>2		=limx−>2
	x−2		x−2

O coś takiego chodzi ?