prosze o pomoc Ania: Ślicznie proszę o pomoc. Byłabym bardzo wdzięczna W graniastosłupie czworokątnym prawidłowym przekątna ściany bocznej ma długość d. Przekątna ściany bocznej i przekątna podstawy poprowadzone z tego samego wierzchołka tworzą kat α. Obliczyć objętość i pole powierzchni bocznej graniastosłupa

Basia: Rysuję

Basia:

	D
cosα=
	d

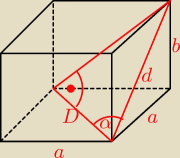
D=dccosα a²+a²=D² 2a² = D²

	D2		d2cos2α
a2 =		=
	2		2

d² = a²+b²

	d2cos2α		2d2−d2cos2α
b2 = d2−a2 = d2 −		=		=
	2		2

d2(2−cos2α)		d2(1+sin2α)
	=
2		2

V = a²*b P_b = 4ab podstaw i wykonaj obliczenia

Ania: a ile wynosi a i b po spierwiastkowaniu? prosze o pomoc

ula: Ania przede wszystkim tam nie ma kąta prostego − już zalożenia są źle zrobione. Tam jest Δrównoramienny o ramionach d i podstawie a√2

Ania: czyli jak mozna to zrobic?

Godzio: tu chyba z tw. cosinusów d² = D² + d² − 2D*d*cosα D² = 2D*d*cosα D = 2d*cosα D = a√2 2d*cosα = a√2 a = d*cosα√2 d² + a² = b² d² + 2d²cos²α = b² d√1 +2cos²α = b V = a² *b = 2d²*cos²α * d√1 +2cos²α = 2d³cos²α√1 +2cos²α P_b = 4*ab = 4*d*cosα√2*d√1 +2cos²α = 4d²√2 cosα*√1 +2cos²α

Ania: dziekuje