trygonometria nachylenie prostej Nikto0: Proszę o pomoc w zadaniu 617 z linka nie wiem co dalej zrobić z tym zadaniem <a href=https://zapodaj.net/d1df84a424ee9.jpg.html>20190627_122940_HDR.jpg</a> <a href=https://zapodaj.net/21167dc930d54.jpg.html>20190627_122904_HDR.jpg</a>

ite:

	−2
prawidłowa odpowiedź cos α =		,
	√5

Twojej odpowiedzi nie mogę odczytać

ite: i nie wiem dlaczego dotyczy innej funkcji (tangesa tego kąta)

Nikto0: Obliczyłam dopiero że tangens alfa równa się minus jedna druga. Czyli to jest zła droga do rozwiązania?

ite:

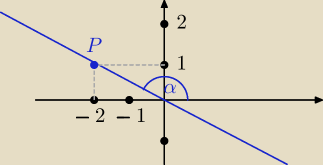
ite: To już widzę, jak chcesz to policzyć. OK, w takim razie teraz skorzystaj z jedynki trygonometrycznej i ze wzoru na tangens, wiesz jak?

Nikto0: Nie wiem.

ite:

	sin α		−1
Trzeba zauważyć, że tg α=		=		i rozwiązać układ równań
	cos α		2

sin²α+cos²α=1

sin α		−1
	=
cos α		2

(nie zmieściło się w klamry)

ite: Masz dwie niewiadome i dwa równania, więc można z tego wyliczyć cos α. Jeśli się naszkicuje prostą w układzie równań (13:05), to wiadomo będzie, że α jest kątem z II ćwiartki. (To się za chwilę przyda.)

6latek: Teraz zauwaz ze OP gdzie O to poczatek ukladu wspolrzednych OP= √x²+y²= √(−2)²+1²=√4+1=√5 Z definicji cosinusa

	x
cosα=		gdzie r=OP
	r

	−2
cosα=
	√5

Patrz rysunek ite

Nikto0: A jedynkę trygonometryczną nie mogę spierwiastkować żeby nie było kwadratów i dalej równała się jeden?

ite: Dzień dobry 6−latku Twój sposób opiera się na innym pomyśle niż ten z układem równań i boję się, żeby to się wszystko nie pomieszało

ite: Nie możesz! Wylicz cos α z drugiego równania i podstaw do pierwszego.

6latek: Dzien dobry W takim razie sie juz nie wypowiadam . Moze tak byc jak napisals .

Nikto0: https://zapodaj.net/df53a39b4b17d.jpg.html mi wychodzi dodatni wynik co robię źle?

ite:

	4
Równanie kwadratowe cos2α=		ma dwa rozwiązania! Trzeba wybrać właściwe, wykorzystując
	5

informację, że α jest kątem II ćwiartki.

Nikto0: Dziękuję za pomoc.

Nikto0: Mam jeszcze jedno pytanie skąd mam wiedzieć do której ćwiartki należy kąt alfa?

ite:

	−x
W zadaniu podane było równianie prostej y=		.
	2

Można tę prostą naszkicować w układzie współrzędnych i zaznaczyć kąt jej nachylenia do osi OX. Można też odczytać (ze wzoru), że prosta będzie przechodzić przez II i IV ćwiartkę (spróbuj to poćwiczyć na innych prostych). Warto tez spróbować policzyć ten cosinus tym sposobem z promieniem wodzącym punktu podanym przez 6latka .

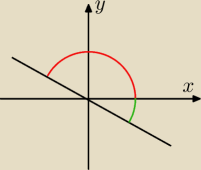
jc: Skąd wiadomo, o który kąt chodzi? zielony czy czerwony. kosinus zielonego kąta > 0 kosinus czerwonego kąta < 0 (kosinusy różnią się znakiem) Nie znamy odpowiedzi D.

ite: Mój błąd, nie zwróciłam uwagi, że jest jeszcze jedna odpowiedź. Wieczorem sprawdzę, co jest napisane w D.

Nikto0: Odpowiedź d jest niepoprawna

ite: A ile wynosi ta ostatnia odpowiedź?

Nikto0: 1 nad pierwiastek z 5

6latek: D jest niepoprawna tgα= −0,5 α= 90^o+27=117^o druga cwiartka

jc: 6latku, prosta przechodzi przez drugą i czwartą ćwiartkę. Dlaczego uważasz, że należy wybrać drugą ćwiartkę?

6latek: Dzien dobry jc Dlatego ze jest to kąt nachylenia prostej y=−0,5x do osi OX

jc: A ten drugi kąt? na moim rysunku zielony.

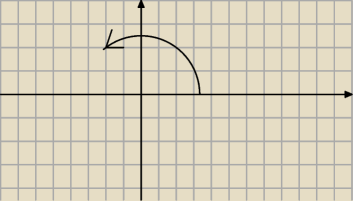
6latek: Bo kat nachylenia oznaczamy tak

jc: Trochę dziwi mnie ta umowa. kąt nachylenia sinusoidy miałby skoki. Malałby od 45^o do zera i nagle zmieniałby się na 180^o i co byłoby dalej?