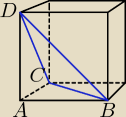
Oblicz odległość wierzchołka A w sześcianie sylwinka90: Witam! Mam problem z tym zadaniem: Narysowany sześcian ma krawędź długości a. Oblicz odległość wierzchołka A od płaszczyzny przechodzącej przez wierzchołki B, C i D. Bardzo proszę o pomoc!

Basia: a jaki to poziom ? szkoła średnia czy studia ? inaczej: czy była już geometria analityczna w przestrzeni trójwymiarowej ?

sylwinka90: Szkoła średnia. Tak prawdę mówiąc to nie wiem za bardzo od czego zacząć w tym zadaniu.

Godzio: a to nie bedzie poprostu wysokość ostrosłupa trójkątnego prawodłowego ?

Anna: Podpowiem chociaż: szukana odległość, to wysokość ostrosłupa prawidłowego trójkątnego BCDA , w którym krawędź podstawy to przekątna kwadratu (czyli a√2 ), a krawędzią boczną jest krawędź sześcianu a. Poradzisz sobie?

Basia: narysuję to inaczej; wtedy będzie widać; poczekaj chwilę

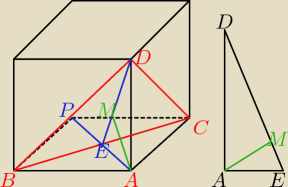
Basia: tr.BDC jest równoramienny ⇒ wysokość DE ma spodek wysokości w środku AP kat EAD jest prosty szukany AM jest wysokością trójkąta prostokątnego EAD o bokach:

	a√2
EA =
	2

AD = a

	2a2		a2		3a2
ED2=EA2+AD2 =		+a2 =		+a2 =
	4		2		2

	a√3		a√6
ED =		=
	√2		2

tr.EMA ≈ tr.EAD

EA		ED
	=
AM		AD

a√2		√6
	=		/*2
2AM		2

a√2
	= √6
AM

	a√2
AM =
	√6

	a√12		2a√3		a√3
AM =		=		=
	6		6		3

moim zdaniem ostrosłup BCDA wcale nie jest prawidłowy tr.BCD jest wprawdzie równoboczny, ale krawędzie boczne nie są równe AB = AC ≠ AE

Basia: sorry błąd; oczywiście jest tak jak napisała Anna; źle odczytałam rysunek; trzeba sobie jednak na kartce narysować

sylwinka90: Dziękuję wam bardzo za pomoc Jestem naprawdę wdzięczna za pomoc Teraz już nawet to rozumiem i zauważyłam te zależności. Jeszcze raz dziękuję