Zadanie
Adrian: Należy podać ilość gram produktu P1 oraz P2, aby po zsumowaniu
mikroskładników każdego z produktów ilość:
białka wyniosła: 75g
węglowodanów wyniosła 248g
Dane dla 100 g produktu:
P1
białko 20g
węglowodany 25g
P2
białko 25g
węglowodany 125g
Odpowiedz to: P1 170 gram, P2 165 gram. Ale jak do tego dojść ?
Może ktoś pomóc mi ułożyć równanie lub wskazać jakiego typu to jest problem.
23 cze 22:48
wredulus_pospolitus:
Układ równań:
P
1 −−− liczba paczek 100g produktu P
1
P
2 −−− liczba paczek 100g produktu P
2
| ⎧ | 20*P1 + 25*P2 = 75 | |
| ⎩ | 25*P1 + 125*P2 = 248 |
|
| | 127 | |
P1 = |
| [*100g] = 169.(3) g |
| | 75 | |
| | 617 | |
P2 = |
| [*100g] = 164.5(3) g |
| | 375 | |
Więc jak już bym zaokrąglał to bym podał: P
1 = 169 g ; P
2 = 165 g
23 cze 23:03
wredulus_pospolitus:
PS .... A tak przy okazji ... jak w 100g produktu P
2 może znajdować się
125g węglowodanów
i jeszcze 25 g białka?
Jak w 100 gramach produktu może być podprodukty o łącznej wadze 150 gram
23 cze 23:06
Adrian: dzięki a powiedz mi czy da się takie zadanie zrobić gdzie suma białek produktów nie jest równa
75,
a węglowodanów 248 tylko jest mniejsza bądź równa i trzeba znaleść jakby najoptymalniejszy
wynik.
23 cze 23:08
Adrian: wreduluspospolitus hehe bardzo spostrzegawczy jesteś przykłady z czapy xD proszę o odpowiedź
do w/w
23 cze 23:09
wredulus_pospolitus:
znaczy się ... chodzi Ci o:
20P
1 + 25P
2 = 'x'
25P
1 + 125P
2 ≤ 248
23 cze 23:12
wredulus_pospolitus:
Można ... ale wtedy nie otrzymujesz jednego wyniku tylko półprostą (a raczej odcinek)
wskazujący proporcję pomiędzy tymi dwoma produktami
23 cze 23:13
Adrian: dokładnie tylko w dwóch miejscach nierówność
23 cze 23:14
Adrian: aha a można za pomocą tego odcinka wywnioskować najlepsze rozwiązanie ?
23 cze 23:14
wredulus_pospolitus:
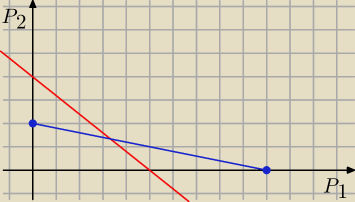
dla ułatwienia:
20P
1 + 25P
2 = 100
25P
1 + 125P
2 ≤
250 <−−− co by były 'ładniejsze liczby'
czerwona prosta reprezentuje pierwsze równanie
niebieski odcinek reprezentuje 25P
1 + 125P
2 = 250
więc więc nierówność spełnia wszystko na niebieskiej linii i 'poniżej niej'.
Częścią wspólną będzie odcinek od przecięcia się czerwonej z niebieską i idącą do osi OP
1 (i
to jest tenże właśnie odcinek)
23 cze 23:17
wredulus_pospolitus:
Nie ma czegoś takiego jak 'najlepsze rozwiązanie' chyba że masz dodatkowo podane jakiś warunek
(np. że w sumie należy zużyć jak najmniej produktów, bądź któryś z produktów jest limitowany
bądź bardziej kosztowny)
23 cze 23:19
wredulus_pospolitus:
Albo np. tak aby węglowodanów było jak najwięcej (przecięcie się prostych/odcinków)
albo węglowodanów było jak najmniej (przecięcie się czerwonej prostej z OP1)
23 cze 23:21
Adrian: warunkiem byłoby to aby suma ilości białka oraz węglowodanów z P1 i P2 była jak największa
nie przekraczając nałożonych ograniczeń.
23 cze 23:34
wredulus_pospolitus:
no to masz przecięcie się tych prostych/odcinków
wtedy masz dla obu nierówności/równości zachowany znak równości
23 cze 23:43
Adrian: ale moze sie zdazyc sytuacja ze nigdy sie nie przetną co wtedy ? Wtedy jak znalesc ten
najbardziej zblizony do maximum?
23 cze 23:59
wredulus_pospolitus:
o ile dwie proste nie są równoległe to ZAWSZE się przetną
24 cze 00:01
wredulus_pospolitus:
a jeżeli dwie proste są równoległe to każda z proporcji zgodna z 'bliższą punktowi (0,0)'
prostą będzie rozwiązaniem
24 cze 00:02
Adrian: a słyszałeś o takiej metodzie jak simplex ? Nadałby się tutaj?
24 cze 00:20
daras: nie gram tylko gramów
24 cze 14:59