planimetria trójkąty
Nikto0: Witam. Proszę o pomoc w zadaniu. Punkty A,B,C są wierzchołkami trójkąta prostokątnego o
przeciwprostokątnej AB, a punkty A, B, M są wierzchołkami trójkąta równobocznego.
Oblicz iloczyn sinusów kątów ostrych trójkąta ABC wiedząc, że pole tego trójkąta ABC jest pięć
razy mniejsze od pola ABM.
Wyszło mi równanie: c do kwadratu razy sin gamma= ab razy sin alfa razy 5. Co dalej? coś mam
źle?
21 cze 16:54
Mila:
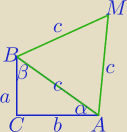
1)
2)
=============
21 cze 17:08
Nikto0: Czyli nie mogę nic uzyskać z mojego równania?
21 cze 17:13
Mila:
Jaki kąt oznaczasz literą γ na moim rysunku?
21 cze 18:18
Nikto0: kąt w trójkącie równobocznym.
21 cze 18:28
Mila:
W Δrównobocznym katy maja po 60 o.
21 cze 18:53
Nikto0: I co z tego wynika?
21 cze 18:59
6latek: Wynika z tego to ze pole trojkata rownobocznego wynosi
===============
Natpmiast pole trojkata prostokatnego ABC≠a*b*sinα
| | 1 | |
Jesli juz to P= |
| *a*b*sin90o bo kąt zawarty miedzy ramionami ai b wynosi 90o |
| | 2 | |
a sin 90
o=1
| | 1 | |
Ostatecznie pole trojkata prostokatnego = |
| *a*b |
| | 2 | |
Takze pole trojkata rownobocznego ≠c
2*sinγ= c
2*sin60
o co jest u Ciebie tylko
| | √3 | | c2*√3 | |
ale sin60o= |
| a to nam daje po przemnozeniu P= |
| |
| | 2 | | 4 | |
21 cze 19:34
Nikto0: Dlaczego pole trójkąta równobocznego to 1/2 razy c do kwadratu razy sin 60 a nie bez 1/2
21 cze 19:45
21 cze 19:47
Nikto0: Dzięki.
22 cze 13:48
 1)
1)