równanie jadwigas: jak rozwiązać równanie sinx=cosx , x∊(0,2π) proszę o pomoc, nie wiem jak to rozwiązać

6latek: zamien cosx na sinx cosx= sin(π/2−x) Dostaniesz sinx= sin(π/2−x) Sinusy sa rowne wtedy kiedy ich argumenty sa rowne Wiec rozwiaz o rownanie Albo sinx−sin(π/2−x)=0 masz wzor na sinx−siny wiec go zastosuj

jc: x=1/4 π lub x=5/4 π

6latek: Dzien dobry jc

jc: Dzień dobry

Mila: sinx=cosx , x∊(0,2π)

	π
x=		+kπ nie spełnia równania,
	2

sinx=cosx /:cosx, cosx≠0

sinx
	=1
cosx

tgx=1 i x∊(0,2π)

	π		π
x=		lub x=		+π
	4		4

6latek: Dobry wieczor Milu Tez potem pomyslaem o tym tangensie .

Mila: Dobry wieczór Twój sposób też poprawny.:

jadwigas: nie zrozumiałam

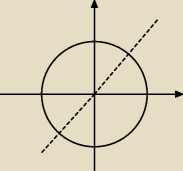
jc: Rysujesz okrąg o promieniu 1. Jedno z ramion kąta, to dodatnia półoś x. Drugie ramie przecina okrąg w punkcie (cos t, sin t). Punkty o równych współrzędnych tworzą prostą x=y, która z kolei daje dwa kąty π/4 oraz 5/4 π.

Mila: tgx=1 to elementarne równanie trygonometryczne, czego tu nie rozumiesz?