trójkąt
majca: W trójkącie prostokątnym ABC o kącie prostym przy wierzchołku C
suma długości przyprostokątnych jest równa m
Na przeciwprostokątnej ( na zewnątrz trójkąta) zbudowano kwadrat
Oblicz odległość punktu C od środka S tego kwadratu
16 cze 20:14
wredulus_pospolitus:
A tenże kwadrat ma bok równy przeciwprostokątnej, czy dowolny

16 cze 20:33
majca:
tak, równy przeciwprostokątnej
pomożesz? pliss
16 cze 21:07
Mila:
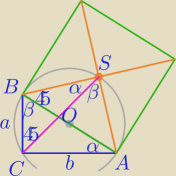
|AB|=c
a+b=m, α+β=90
o
2) Na czworokacie CASB można opisać okrąg.
∡ASB=90
o
Z sumy kątów w ΔCBS ⇒|∡CBS=45
o|⇔CS jest dwusieczną kąta C.
Licz długość |CS|
16 cze 21:09
Eta:
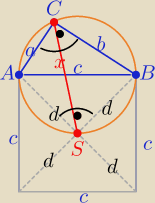
a+b=m , d=
√2c/2
na czworokącie ASBC można opisać okrąg
z tw. Ptolemeusza
|AS|*|CB|+|AC|*|BS|=|AB|*|SC| , |SC|=x , |AB|=c |AS|=|BS|=d=
√2c/2
to
| √2 | | √2 | | √2 | |
| c*b+ |
| c*a=c*x /: c>0 ⇒ x= |
| (a+b) |
| 2 | | 2 | | 2 | |
♥♥♥♥♥♥♥♥♥♥♥♥
16 cze 21:24
Mila:
Ten sam miałam pomysł, ale obliczyłam kąty, aby mogła majca inaczej obliczyć.
16 cze 21:32
an:
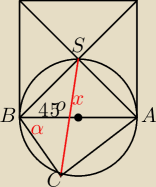
| | AC+BC | | m | |
sinα +cosα= |
| = |
| |
| | BA | | 2R | |
| | 1 | |
Z tw. sinusów CS=2Rsin(45+α)=2R(sin45cosα+cos45sinα)=2R |
| (cosα+sinα)= |
| | √2 | |
| 2R | | AC+BC | | 2R | | m | | √2 | |
| |
| = |
| |
| = |
| m |
| √2 | | BA | | √2 | | 2R | | 2 | |
17 cze 14:01
Eta:

17 cze 20:15

 |AB|=c
a+b=m, α+β=90o
|AB|=c
a+b=m, α+β=90o
 a+b=m , d=√2c/2
na czworokącie ASBC można opisać okrąg
z tw. Ptolemeusza
|AS|*|CB|+|AC|*|BS|=|AB|*|SC| , |SC|=x , |AB|=c |AS|=|BS|=d=√2c/2
to
a+b=m , d=√2c/2
na czworokącie ASBC można opisać okrąg
z tw. Ptolemeusza
|AS|*|CB|+|AC|*|BS|=|AB|*|SC| , |SC|=x , |AB|=c |AS|=|BS|=d=√2c/2
to

