Rachunek pp Pawlo: 1. O zdarzeniach A,B wiemy że P(A) = 0,8 i P(B) = 0,3. Minimalna wartość P(A∩B) wynosi? Wydaje mi się, że 0. Czy mógłby mnie ktoś upewnić w tym? 2. X ma rozkład N(−1,2). Największe prawdopoodbieństwo ma zdarzenie: a) −4<x<−3 b) −5<x<−4 c) −2<x<−2 d) −3<x<−2 Nie wiem jak się za to zabrać w ogóle. 3. Zmienna losowa X ma funkcje charakterystyczną φ(t) = (jakas tam funkcja) P(X=1) wynosi? (ogólnie chodzi mi o sposób rozwiązania takiego zadania) 4. Zmienna losowa X ma rozklad poissona. Wiadomo, że F(1) = 1/8. ile wynosi EX? 5. Gestosc zmiennej losowej ciagle X wyraza sie wzorem ( tutaj wzor ). Niech Y = X². Oblicz EY Potrzebuje wskazówek/ sposobów rozwiązania zadań tego typu. Z góry dzięki!

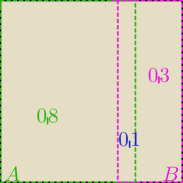
iteRacj@: Minimalna wartość P(A∩B) to 0,1. Maksymalna 0,3.

iteRacj@: Resztę już ktoś inny podpowie, ja wychodzę : )

Pawlo: Okay dzięki iteRacj@ Myślałem, że to bardziej podchwytliwe

Pawlo: Ktoś coś?

wredulus_pospolitus: 2. Tak na 'chłopski rozum'. Pomijając (c) wszystkie inne odpowiedzi mają przedział długości '1' więc prawdopodobieństwo będzie miał przedział, który jest 'najbliżej' EX = −1 Dlatego odp (d)

wredulus_pospolitus: 3. Jeżeli X ma rozkład ciągły to f(X=k) = 0 (prawdopodobieństwo otrzymania KONKRETNEJ wartości wynosi 0)