nierówność wymierna paka: miałam nierówność i doszłam do takego:

x3+1
	≤0
(x−1) (x+1)

(x³+1) (x−1) (x+1)≤0 i nie wiem co dalej

iteRacj@: Musisz określić dziedzinę tej nierówności, tylko wtedy obie postaci będą równoważne. Zastosuj wzór skróconego mnożenia dla x³+1=

paka: D: R\ [−1;1] (x+1)(x²−x+1)(x−1)(x+1)≤0 tak?

PW: Najpierw skróć ułamek przez (x+1), będzie łatwiej.

wredulus_pospolitus: 1) wzór skróconego mnożenia: x³ + 1 = (x+1)(x² − x + 1) 2) skracamy

(x+1)(x2−x+1)		x2−x+1
	=
(x−1)(x+1)		x−1

3) x²−x+1 > 0 dla dowolnego 'x' (ponieważ Δ < 0 i a=1>0) 4) w takim razie ów nierówność kiedy będzie spełniona

jadwigas: dlaczego taki znak w pkt 3?

jadwigas: myślałam, że ma być taki sam znak jak w początkowej nierówności

jadwigas: no rozumiem że delta jest mniejsza od zera, nie wiem kiedy ta nierówność będzie spełniona

jadwigas: haloo?

paka: tak, też nie wiem co jeżeli Δ < 0 i a=1>0

paka: heelp

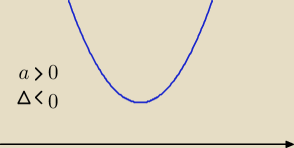
iteRacj@: → brak miejsc zerowych

paka: a, a wtedy jaka ma być odpowiedź?

6latek: Jadwisiu w czym masz problem? Mozesz zrobic tak jak w tamtej nierownosci ale po wymnozeniu dostaniesz nierownosc stopnia trzeciego Potem miejsca zerowe i fala Mozesz tez podejsc do tego z innej strony tak jak proponuje wredulus x²−x+1 jest zawsze dodatnie (to co napisal )

	x2−x+1
Wiec nierownosc		ma byc mniejsza od zera
	x−1

Licznik jest zawsze dodatni to jak to nierownosc bedzie gdy mianownik bedzie dodatni? Licznik jest zawsze dodatni to jak ta nierownosc bedzie gdy mianownik bedzie ujemny ?

iteRacj@: dziedzinę trzeba zapisać tak D = R\ {−1;1}

	x3+1		x2−x+1
wyrażenie		można zapisać w postaci
	(x−1)(x+1)		x−1

wtedy licznik przyjmuje wyłącznie wartości dodatnie,

	x2−x+1
więc → 1) widać że nierówność		≤0 nie przyjmie wartości 0;
	x−1

→ 2) trzeba sprawdzić, dla jakich argumentów przyjmie wartości ujemne i tu widać, że znak wyrażenia będzie zależeć tylko od znaku mianownika.

iteRacj@: *powinno być wyrażenie nie przyjmie wartości 0

paka: czyli co mam napisać w końcu? Δ<0, brak miejsc zerowych x−1≠0 x≠1 to jaka ostateczna odpowiedź? D: R\ 1 ?

paka: jak sprawdzić to dla jakich argumentów przyjmie wartości ujemne

6latek: Dobry wieczor iteRacj@ Nie czytasz to co sie do Ciebie pisze tylko chcesz gotowe rozwiazanie Musisz rozwiac nierownosc x−1<0 bo wtedy cala nierownosc bedzie <0

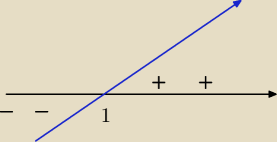
iteRacj@: w mianowniku jest wyrażenie x−1 musisz rozwiązać nierówność x−1<0

iteRacj@: Dobry wieczór Staram się czytać, to co do mnie piszą : ))) Ale nie umiem wytłumaczyć, o co tu chodzi.

6latek: Ale to nie byla uwaga do Ciebie

iteRacj@: Ale zawsze chętnie przyjmuje gotowe rozwiązania.

6latek: Oczywiscie ja rownież

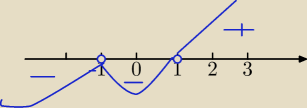
Mila: D=R\{−1,1} (x³+1) (x−1) (x+1)≤0⇔ (x+1)*(x²−x+1)*(x−1)*(x+1)≤0⇔ (x²−x+1)*(x+1)²*(x−1)≤0 f(x)=x²−x+1 parabola skierowana do góry i Δ=1−4=−3<0⇔f(x) przyjmuje tylko wartości dodatnie, nie wpływa na zmianę znaku wyrażenia: (x²−x+1)*(x+1)²*(x−1) Zatem nierówność jest równoważna nierówności: (*) (x+1)²*(x−1)≤0 x∊(−∞,−1)∪(−1,1)

6latek: Dobry wieczor Milu Wlasnie u nas przestalo padac .

Mila: O, to zazdroszczę tego deszczu, my się topimy z upału