proszę o rozwiązanie anna: dany jest trójkąt ABC Punkt S jest środkiem boku AB tego trójkąta Wykaż że odległości punktów A i B od prostej CS są równe

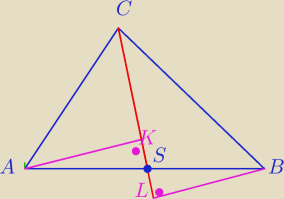
janek191: Wskazówka : pokaż,że Δ AKS i Δ BLS są przystające.

anna: czy wystarczy napisać △ AKS ≡ △ BLS ( kkk) bo ¬KSA = ¬BSL kąty wierzchołkowe ¬AKS = ¬BSL = 90₀ czyli AS = BS cnd

Saizou : 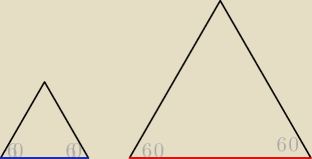anna napisałaś cechę podobieństwa a nie przystawania. Figury podobne mają własność kkk, ale nie muszę być tych "samych rozmiarów" (zobacz rysunek trójkątów równobocznych). Z tego nie wynika, że odcinki niebieski i czerwony mają równe długości

Mariusz: Skoro S jest środkiem boku AB to AS=SB

Mariusz:

	xA+xB		yA+yB
S=(		,		)
	2		2

(AS)²=

	xA+xB		yA+yB
(xA−		)2+(yA−		)2
	2		2

	(xA+xB)2
x2A−xA(xA+xB)+		+
	4

	(yA+yB)2
y2A−yA(yA+yB)+
	4

	x2A		xB
x2A−xA(xA+xB)+		+		(2xA+xB)
	4		4

	y2A		yB
+y2A−yA(yA+yB)+		+		(2yA+yB)
	4		4

5		xB
	x2A−xA(xA+xB)+		(2xA+xB)
4		4

	5		yB
+		y2A−yA(yA+yB)+		(2yA+yB)
	4		4

	5		xB
(SA)2=		x2A−xA(xA+xB)+		(2xA+xB)
	4		4

	5		yB
+		y2A−yA(yA+yB)+		(2yA+yB)
	4		4

	xA+xB		yA+yB
(SB)2=(xB−		)2+(yB−		)2
	2		2

	x2B+(2xB+xA)xA
=x2B−xB(xA+xB)+		+
	4

	y2B+(2yB+yA)yA
y2B−yB(yA+yB)+		+
	4

5		xA
	x2B−xB(xA+xB)+		(2xB+xA)+
4		4

5		yA
	y2B−yB(yA+yB)+		(2yB+yA)
4		4

janek191: Na podstawie cechy kkk trójkąty są podobne. AS = SB więc skala podobieństwa k = 1, zatem również KS = LS oraz AK = BL =========

Mariusz: Trójkąty podobne , długości odpowiednich boków są proporcjonalne Trójkąty przystające , długości odpowiednich boków są równe Wpis z 13 cze 2019 09:20 może być uzasadnieniem dlaczego AS=SB gdy S jest środkiem boku AB janek191 Czy punkty K oraz L tak dobrałeś aby KS = SL Jeśli tak to mielibyśmy oprócz równości kątów równość dwóch boków a jeśli nie to oprócz równości kątów mamy równość jednego boku

anna: dziękuję wszystkim za cenne wskazówki