równanie okręgu opisanego na trójkącie jadwigas: Dany jest trójkąt o wierzchołkach A(2,2), B(−2,4), C(−1,5) napisać równianie okręgu opisanego na tym trójkącie Obliczyłam już odległośćpunktów : IABI=√20 = 2√5, IBCI=√2, IACI=3√2 równanie (x−a)²+(y−b)² ≥ r r = √5 nie wiem co robić dalej , trzeba znależć środek, jak to zrobić , nie rozumiem

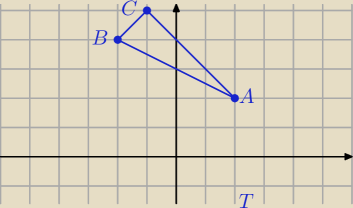
janek191: To jest Δ prostokątny, bo 18 + 2 = 20 więc r = 0,5 I AB I = √5 S = ( 0, 3) − środek odcinka AB ( x − 0)² = ( y − 3)² = 5 ===================

janek191: Poprawka x² + ( y − 3)² = 5

ite: 16:22 nierówność (x−a)²+(y−b)² ≥ r² opisuje okrąg i jego zewnętrze

jadwigas: a jak znalazłeś środek okręgu?

jadwigas: jest tu ktoś?

janek191: A = ( 2, 2) B = ( −2, 4) więc

	2 + (−2)
xs =		= 0
	2

	2 + 4
ys =		= 3
	2

S = ( x_s, y_s) = ( 0, 3)