| 1 | ||
r = | a√2 | |
| 2 |
| 1 | ||
P = 4 * π( | a)2 − (πr2 − a2) = 2πr2− πr2 − 2r2 = πr2 − 2r2 = r2(π − 2) | |
| 2 |
| π 22 | π (2√2)2 | |||
a) 22 + 2 | − | = 4 | ||
| 4 | 4 |
 Jeżeli oto to zauważ że masz okrąg opisany na kwadracie ... czyli jego środek leży w przecięciu
przekątnych, przekątne w kwadracie przecinają się pod kątem 90o związku z tym możesz zobaczyć
trójkąt prostokątny o przyprostokątnych r i r oraz przeciwprostokątnej a
z tw. Pitagorasa: a2 = r2 + r2 −> a2 = 2r2
Jeżeli oto to zauważ że masz okrąg opisany na kwadracie ... czyli jego środek leży w przecięciu
przekątnych, przekątne w kwadracie przecinają się pod kątem 90o związku z tym możesz zobaczyć
trójkąt prostokątny o przyprostokątnych r i r oraz przeciwprostokątnej a
z tw. Pitagorasa: a2 = r2 + r2 −> a2 = 2r2
| 1 | 1 | |||
4*π( | a)2 oznacza tyle co: 4 razy pole okręgu o promieniu | a ... a przecież tam | ||
| 2 | 2 |
| a | ||
liczysz 4* POŁOWA pola okręgu o promieniu | ||
| 2 |
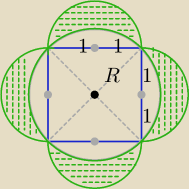 Pole księżyców Hipokratesa:
R=√2
1) Pole całej figury:
Pf=22+2*π*12=4+2π
2) Pole księżyców:
Pk=Pf−π*R2=4+2π−π*(√2)2
Pk=4
Wniosek: ?
Pole księżyców Hipokratesa:
R=√2
1) Pole całej figury:
Pf=22+2*π*12=4+2π
2) Pole księżyców:
Pk=Pf−π*R2=4+2π−π*(√2)2
Pk=4
Wniosek: ?
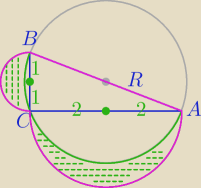 b)
|AB|2=22+42=20, |AB|=2√5
R=√5
1)
Pole figury o różowym brzegu
Pf=PΔ+Pola dwóch półkoli
b)
|AB|2=22+42=20, |AB|=2√5
R=√5
1)
Pole figury o różowym brzegu
Pf=PΔ+Pola dwóch półkoli
| 1 | 1 | 1 | ||||
Pf= | *2*4+ | *π*12+ | *π*22 | |||
| 2 | 2 | 2 |
| 5 | ||
Pf=4+ | π | |
| 2 |
| 5 | 1 | |||
Pk=4+ | π− | *π*(√5)2 | ||
| 2 | 2 |