Planimetria Jaskier: Dobry wieczór Takie zadanie z pdr do matmy i już siedzę nad nim godzine i wydaję mi się że jest sprzeczne. Okrąg o promieniu 6 opisano na czworokącie ABCD. Boki AD i DC mają równe długości, a kąt ABC ma miarę 120. Oblicz pole tego czworokąta, jeśli stosunek pól trójkątów ABD i BCD jest równy 2 :1. Wystarczy mi jak ktoś powie czy to ma sens czy nie

wredulus_pospolitus: szczerze mówiąc to nie widzę problemu w tym zadaniu ... możesz pokazać gdzie widzisz sprzeczność ?

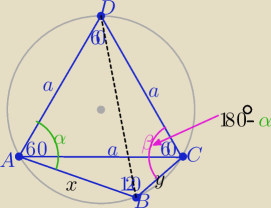
Eta: 1/ rysunek 2/ z warunku wpisania czworokąta w okrąg sumy miar kątów przeciwległych są równe 180^o zatem trójkąt ACD jest równoboczny wpisany w okrąg o promieniu R=6

	a√3
3/R=		⇒ .... a=6√3
	3

4/ z treści zadania

P(ABD)		ax*sinα
	=2 ⇒		=2 ⇒ x=2y bo (sinα=sinβ)
P(BCD)		ay*sinβ

5/ztw. cosinusów w ΔABC a²= ................................ a²=7y² ⇒ y²=36*3/7 P(ABCD)=P(ACD)+P(ABC)=............... dokończ P(ABCD)= 243√3/7 ===============

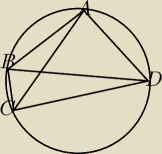
Jaskier: (P_ABD) \ (P_BCD) =AB\BC=2 poniewać AB=2BC ∠ADB=2∠BDC ⇒ ∠ADB= 40, ∠BDC =20 (P_ABD) \ (P_BCD)= (BD*AD*sinBDA)/(BD*CD*sinBDC)=sin40/sin20=2 2sin20cos20=2sin20 cos20=1?

Eta: Bzdury napisałeś!