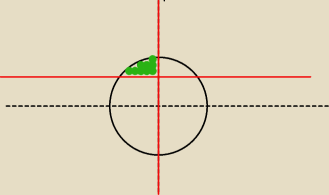
Wprowadzając współrzędne biegunowe obliczyć podane całki, po danym obszarze D. xyz: Wprowadzając współrzędne biegunowe obliczyć podane całki, po danym obszarze D. int int 1/[(x²+y²)²] dxdy D: x²+y²=4, x<=0, y>=1 Obszar wygląda mniej więcej tak: (patrz rysunek) Pytanie jak ograniczyć r? 0d 0 do −sqrt(4−rsin@)

jake: .

ads: ?

jc: Całka nie ulegnie zmianie, jeśli obrócimy obrazek o 90 stopni. x²+y² ≤4, y≥0, x ≥1 x = r cos t y = r sin t

1
	≤ r ≤ 2
cos t

0 ≤ t ≤ π/3

	r dr
całka = ∫0π/3 dt ∫21/cos t
	r4

	1
=		∫0π/3 [cos2t − 1/4 ] dt = ....
	2

xyz: to w takim razie nie powinno być 0≤t≤π/2 ?

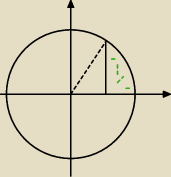
jc: Kąt zaznaczony przerywaną linią = 60^o

xyz: No dobra ale przy ograniczaniu r nie powinno być 1/sin t ? bo mamy prostą y=1 rsint=1 r=1/sin t

jc: Obróciłem i jest cos t (pamiętaj, nie cost). Teraz mamy x ≥ 1 w miejsce y ≥ 1.

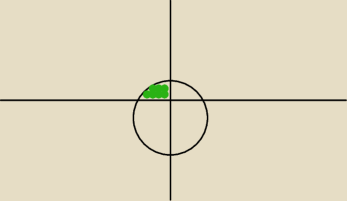
xyz: zgadza, teraz widzę. A czy można przykombinować tak żeby ten obszar zaczął się w środku układu współrzędnych? kąt będzie ograniczony w ten sposób: π/2≤t≤π a promień: 0≤r≤ no właśnie. Jeżeli we wzorze x²+y²=4 zamienię współrzędne na biegunowe to wychodzi mi r²=4

jc: Mógłbyś początek biegunowego układu współrzędnych umieścić na okręgu, w szczególności na końcu zielonego pola. Wydaje mi się, że każde inne położenie da nieprzyjemne rachunki.