planimetria zadanie otwarte trójkąt Nikto0: Witam. Proszę o pomoc w zadaniu. Przyprostokątne trójkąta prostokątnego mają długości 3 cm i 4 cm oblicz sinus kąta jaki tworzy wysokość opuszczona na przeciwprostokątną z najkrótszym bokiem tego trójkąta. Który to jest kąt którego mam obliczyć sinus i dlaczego ten a nie inny

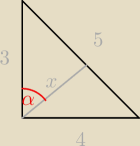
wredulus_pospolitus: ten kąt

wredulus_pospolitus: masz podane kąt jaki tworzy WYSOKOŚĆ (długości 'x') z najkrótszym bokiem (czyli o długości '3')

Nikto0: A jakiś sposób na rozwiązanie tego zadania?

janek191: P = 0,5*3*4 = 6 P = 0,5*5*x = 2,5 x = 6

	6		12
x =		=		= 2,4
	2,5		5

	x		2,4		24		4
cos α =		=		=		=
	3		3		30		5

	16		9
sin2 α = 1 − cos2 α = 1 −		=
	25		25

	3
sin α =
	5

Nikto0: A z wysokości poprowadzonej z wierzchołka kąta prostego która dzieli przeciwprostokątną na odcinki też da się to wyliczyć? albo z podobieństw trójkątów?

ite:

	ab
Możesz obliczyć tę wysokość ze wzoru x=hc=		, c − przeciwprostokątna, a,b −
	c

przyprostokątne. Wzór jest w tablicach maturalnych. A potem wyliczyć sin α, niewiele się to różni od sposobu janka.

Nikto0:

	x		3
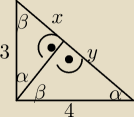
czy nie z podobieństw trójkątów ja tak robiłam sinα=		=
	3		x+y

ite:

	3
Możesz liczyć z podobieństwa trójkątów sin α =		najszybciej.
	x+y

	x
Z zależności sin α =		więcej liczenia: musisz najpierw wyliczyć hc − wysokość
	3

opuszczoną na przeciwprostokątną, a potem x np. z tw.Pitagorasa.

Nikto0: Nie wiem co mam źle w moim sposobie może ktoś wyjaśnić moje rozwiązanie w linku https://zapodaj.net/04a91f679eab6.jpg.html

ite: Zauważenie, że szukany kąt α ma taką samą miarę jak kąt pomiędzy dłuższą przyprostokątną a przeciwprostokątną w wyjściowym Δ, jest najkrótszym sposobem znalezienia rozwiązania. Po co jeszcze dalej coś liczyć?

Nikto0: w celach edukacyjnych

Nikto0: To co jest źle?

ite: słuszny cel h_c=2,4 (z wyliczeń janka) a nie 4

ite: źle odczytałam drugie równanie, tam jest h² a nie 4²

Nikto0: Czyli co z tym zadaniem? bo nie rozumiem

Bleee:

	3
Tak... Można było pokazać z podobieństwa trójkątów że sinα =
	5

Nikto0: ale z tym sposobem w linku

ite:

	9		y2
zupełnie nie wiem, skąd się wzięło		=
	16		x2

Nikto0: po podzieleniu tak nie można robić?

ite: ? ? ? nie ma prawa wyjść taki ułamek

Nikto0: dzielę 16/9 dzielę h² przez h² i y² przez x²

ite:

	h2+y2
dzielisz		?
	x2+h2

Nikto0: i 16 przez 9

ite: 15:54 nic nie da się uprościć !

Nikto0: to jak to zrobić?

ite: Nie mam już czasu tego pisać, zaraz muszę wychodzić. Może ktoś to wyjaśni.

Nikto0: ok.Dzięki.

Nikto0: Pytanie do innych czy kiedykolwiek mogę tak podzielić w układach równań?

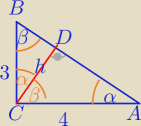
Mila: ΔCDB∼ΔACB |AB|=5

	3
sinα=
	5