Prawdopodobieństwo
Paweł: Na ile sposobów może usiąść przy okrągłym stole 5 dziewcząt i 5 chłopców tak, aby obok siebie
nie siedziały osoby tej samej płci?
| | 5!*5! | |
Myślałem, że powinno być 5! * 5!, ale wynik to |
| = 5!*4!... Dlaczego tak? |
| | 5 | |
10 cze 09:38
Paweł:
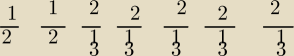
I jeszcze jeden podpunkt. Ile różnych liczb 7−cyfrowych można zapisać za pomocą cyfr 1, 2, 3
tak, aby cyfra
2 występowała dokładnie dwa razy.
10 cze 09:48
wredulus_pospolitus:
a)
na:
5!*4! sposobów ponieważ:
pierwszy (konkretny) chłopak siada na dowolnym miejscu ... jako że jest to okrągły stół (a
krzesła nie są rozróżnialne), to wszystkie miejsca są 'jednakowe' ... dlatego siada on na [C[1
sposób]]
staje on się w tym momencie 'punktem odniesienia'.
Po prawej od niego siada jedna z 5 dziewczyn, na prawo od niej jeden z 4 chłopaków, itd.
10 cze 10:52
wredulus_pospolitus:
b) jest ok
10 cze 10:53
Paweł: A jeśli ustawić by ich w rzędzie? Też na przemian
10 cze 11:18
piotr: krzesła są o tyle rozróżnialne, że stoją w określonym miejscu (np. opisanym kątem)
chyba, że stół i krzesła znajdują się poza jakimikolwiek układem odniesienia, a dodatkowo
krzesła są ustawione względem stołu tak, że obrót wokół osi stołu o kąt n*72o jest
"niezauważalny"
10 cze 11:20
Paweł:
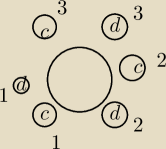
Poza tym nie bardzo rozumiem ten a) niestety. Powiedzmy, że jest 3 chłopców i 3
dziewczyny(łatwiej będzie narysować)
Czyli wychodzi 3!*3! Przynajmniej ja to tak rozumiem :<
10 cze 11:32
wredulus_pospolitus:
Paweł −−− dla 3 chłopów (A,B,C) i 3 dziewczyn (d,e,f)
układy:
(A,d,B,e,C,f) oraz (d,B,e,C,f,A) TO SĄ TE SAME UKŁADY, a Ty je liczysz jako dwa oddzielne
tak samo jak (C,f,A,d,B,e) itd.
Jakbyś ludzi ustawił w rzędzie to byłoby 2*5!*5! sposobów (ów 2 odpowiada temu: "kto
pierwszy stoi, chłop czy dziewoja")
10 cze 11:47
Paweł: No tak, teraz wszystko rozumiem! Dziękuje

10 cze 11:51
wredulus_pospolitus:
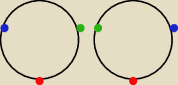
Paweł to może inaczej −−− na ile sposób można usadzić przy okrągłym stole (3 krzesła) 3 różne
osoby?
Na 2! = 2 sposobów:
Albo czerwony ma 'po lewej' niebieski, albo zielony. Obrócenie stołu nic nie zmienia bo
sytuacja jest taka sama jak jedna z powyższych
10 cze 11:51
wredulus_pospolitus:
Musisz zapamiętać, że w tego typu zadaniach (okrągły stół vel karuzela) pierwsza osoba
siadająca staje się 'punktem odniesienia' dla wszystkich kolejnych siadających osób
10 cze 11:52
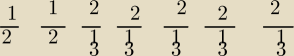 I jeszcze jeden podpunkt. Ile różnych liczb 7−cyfrowych można zapisać za pomocą cyfr 1, 2, 3
tak, aby cyfra
2 występowała dokładnie dwa razy.
I jeszcze jeden podpunkt. Ile różnych liczb 7−cyfrowych można zapisać za pomocą cyfr 1, 2, 3
tak, aby cyfra
2 występowała dokładnie dwa razy.
 Poza tym nie bardzo rozumiem ten a) niestety. Powiedzmy, że jest 3 chłopców i 3
dziewczyny(łatwiej będzie narysować)
Czyli wychodzi 3!*3! Przynajmniej ja to tak rozumiem :<
Poza tym nie bardzo rozumiem ten a) niestety. Powiedzmy, że jest 3 chłopców i 3
dziewczyny(łatwiej będzie narysować)
Czyli wychodzi 3!*3! Przynajmniej ja to tak rozumiem :<

 Paweł to może inaczej −−− na ile sposób można usadzić przy okrągłym stole (3 krzesła) 3 różne
osoby?
Na 2! = 2 sposobów:
Albo czerwony ma 'po lewej' niebieski, albo zielony. Obrócenie stołu nic nie zmienia bo
sytuacja jest taka sama jak jedna z powyższych
Paweł to może inaczej −−− na ile sposób można usadzić przy okrągłym stole (3 krzesła) 3 różne
osoby?
Na 2! = 2 sposobów:
Albo czerwony ma 'po lewej' niebieski, albo zielony. Obrócenie stołu nic nie zmienia bo
sytuacja jest taka sama jak jedna z powyższych