ekstrema funkcji kers02: Jak wyznaczyć ekstema funkcji?

	x−2
f(x)=
	√x2+1

	2x+1
Pochodna wyszła mi		. Jak bez rysowania wykresu tej funkcji, mogę
	(x2+1) √x2+1

policzyć ekstrema, monotonicznosc?

Jerzy: Możesz pokazać, jak liczysz pochodną.

Bleee: O ile pochodną dobrze wyznaczona to wystarczy zauważyć że mianownik zawsze przyjmuje wartości dodatnie. Tak więc interesuje Ciebie tylko wartość licznika (w celu wyznaczenia monotonicznosc i ekstrem funkcji f(x))

Bleee:

	g(x)
W przypadku funkcji f(x) =
	h(x)

Po obliczenia pochodnej i NIE WYKONYWANIU ŻADNYCH PRZEKSZTAŁCEŃ mianownik Zawsze będzie przyjmować tylko wartości dodatnie

kers02: z licznika wychodzi x=1/2 i co z tym mogę zrobić?

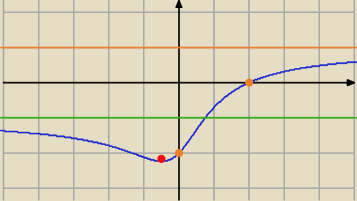
piotr: lim_x−>−∞ = −1 ⇒ asymptota pozioma y= −1 dla x<−1/2 f(x) malejąca dla x=−1/2 maksimum f(−1/2) = −√5 dla x>−1/2 f(x) rosnaca f(0) = −2 f(2) = 0 lim_x−>∞ = 1 ⇒ asymptota pozioma y= 1

kers02: Niestety to nie wiele mi pomogło. Skąd mogę wiedzieć że f jest na tych przedziałach rosnaca/malejaca itp? skąd to się wzieło?

Mila: f'(x)>0 ⇔f(x) jest rosnąca

	1		1
2x+1>0⇔x>−		⇔f(x) jest rosnąca dla x∊(−		,∞)
	2		2

	1
f'(x)<0⇔f(x) jest malejąca dla x<−
	2

	1
Dla x=−		funkcja ma ekstremum,
	2

	1
Przy przejściu przez x=−		pochodna zmienia znak z ujemnego na dodatni zatem
	2

	1
dw x=−		jest minimum.
	2