 Rozwiązania dzisiaj już nie chce mi się pisać ( może jutro.. jak nikt wcześniej nie poda
Rozwiązania dzisiaj już nie chce mi się pisać ( może jutro.. jak nikt wcześniej nie poda 
| 3 | ||
Odp: S= | P | |
| 40 |


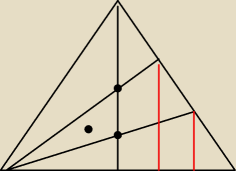 Wysokość trójkąta =1, wyższa kropka = x, niższa = y.
Proporcje:
x:(2/3) = (1/2):(2/3), x=1/2
y:(1/3) = (1/2):(5/6), y=1/5
x−y=3/10, taką część lewego trójkąta zajmuje trójkąt z kropką.
Pole lewego trójkąta = pole równoległoboku /4
Stąd mamy 3/40.
Wysokość trójkąta =1, wyższa kropka = x, niższa = y.
Proporcje:
x:(2/3) = (1/2):(2/3), x=1/2
y:(1/3) = (1/2):(5/6), y=1/5
x−y=3/10, taką część lewego trójkąta zajmuje trójkąt z kropką.
Pole lewego trójkąta = pole równoległoboku /4
Stąd mamy 3/40.
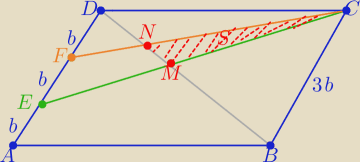
 1/ Z podobieństawa trójkątów
DFN i BCN w skali k=1/3 i trójkątów EDN i BCM w skali w= 2/3
P(BDC)= 12P , P=p(ABCD)
2/ trójkąty DNC, DMC, DBC mają wspólną wysokość
to
1/ Z podobieństawa trójkątów
DFN i BCN w skali k=1/3 i trójkątów EDN i BCM w skali w= 2/3
P(BDC)= 12P , P=p(ABCD)
2/ trójkąty DNC, DMC, DBC mają wspólną wysokość
to
| P(DBC) | DB | DN+NB | NB | ||||
= | = | = 1+ | = 1+3=4 | ||||
| P(DNC) | DN | DN | DN |
| 1 | 1 | |||
zatem P(DNC)= | P(DBC)= | P | ||
| 4 | 8 |
| P(DBC) | DB | DM+BM | MB | 3 | |||||
= | = | =1+ | =1+ | = 5/2 | |||||
| P(DMC) | DM | DM | DM | 2 |
| 2 | 1 | |||
zatem P(DMC)= | P(DBC)= | P | ||
| 5 | 5 |
| 1 | 1 | |||
S=P(DMC)−P(DNC)= | P− | P | ||
| 5 | 8 |
| 3 | ||
S= | P | |
| 40 |
| 1 | ||
BC : DF=3=BN : DN, DN= | DB | |
| 4 |
| 2 | ||
DE : BC=3 : 2=BM : DM, DM= | BD | |
| 5 |
| 2 | 1 | 3 | ||||
NM= | BD− | BD= | BD | |||
| 5 | 4 | 20 |