5 cze 20:56
wredulus_pospolitus:
TABLICE TRYGONOMETRYCZNE

5 cze 21:14
XYZ: Chodzi o to by obliczyć przy użyciu własności trygonometrycznych oraz znajomości wartości sin,
cos, tg, ctg wylaczenie dla 0, 30, 45, 60, 90 stopni
5 cze 21:18
xyz:
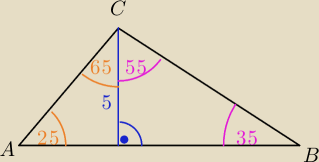
5 cze 21:33
xyz:
nie da sie tylko dla tych co opisales.
nawet to tw. sinusow trzeba znac inne...
5 cze 21:37
XYZ: I jak obliczyć długość boku AC?
5 cze 21:37
wredulus_pospolitus:
Ponownie napiszę: TABLICE TRYGONOMETRYCZNE

Niby gdzie masz podane, że masz obliczyć korzystając z kątów 30,45,60

5 cze 22:00
sin:
sin25o=5/AC , sin25o≈0,4226
AC=5/sin25o
AC= ..........................................
5 cze 22:10
XYZ: To zadanie ze sprawdzianu i dostępna była tylko tabela z kątami 0,30,45,60,90...
5 cze 22:13
XYZ: ehh
5 cze 22:24
wredulus_pospolitus:
a miałeś dostęp do jakiegokolwiek kalkulatora (nawet najprostszego)

5 cze 22:34
wredulus_pospolitus:
a gdzie tam
szacowanie nie będzie wystarczające (dokładność 0.5 cm oznacza, że wartość sin25o trzeba
oszacować z dokładnością około 0.02)
skoro zarzekasz się, że nie było możliwości zajrzenia jaką wartość mają funkcje
trygonometryczne kątów 25o czy też 65o to idź jutro do nauczyciela/−ki by wyjaśnił/−a jak
zrobić to zadanie
5 cze 22:40
wredulus_pospolitus:
dobra ... znalazłem sposób na oszacowanie tego w taki sposób aby uzyskać wynik z dokładnością
0.5 cm, ale jest to 'mocno naciągany' sposób i wątpię by oto chodziło w zadaniu. Dodatkowo
wątpię by na poziomie (podejrzewam) liceum ktokolwiek był w stanie to odpowiednio
uargumentował.
5 cze 22:53
an: | | 5 | | 5 | |
Z w wystarczająca dokładnością jak do tego sin25≈ |
| sin30= |
| |
| | 6 | | 12 | |
AC≈12 z dokładnością ≈0,17cm, a więc 3 krotnie lepszą od wymaganej, moim zdaniem
wyjaśnienie >> na wykresie prosta styczna do funkcji sin w punkcie 30
o na odcinku
od 10
o do 45
o odwzorowuje wartość sinusa z dokładnością lepszą od 3%<<, czy to mieści się
w zakresie wymaganej wiedzy XYZ, nie wiem
6 cze 12:51
ABC:
interpolacja liniowa to chyba nie w obecnej szkole

6 cze 13:03
wredulus_pospolitus:
an o tym własnie myślałem, ale wtedy rodzą się jednak takie problemy:
| | 5 | |
1) co mógłby uczeń zrobić to ocenić, że sin25o > |
| ≈ 0,41(6) na podstawie wykresów y=x |
| | 12 | |
oraz y=sinx
2) to że w tym przypadku możesz napisać |AC| ≈ 12 i jest to poprawny wynik jest tak naprawdę
strzałem
bo wystarczy, że sin25
o = 0,43478 a nie 0.4226 (a przecież uczeń nie wie ile wynosi sinus tego
kąta) i byłbyś poza przedziałem dokładności.
3) ale w tym momencie wiemy tylko że 10 < |AC| < 12
więc już bezpieczniejszym wyjściem będzie podanie |AC| ≈ 11.5 ponieważ daje nam to 'przedział'
długości 1 a nie tylko 0.5.
Ale nadal tutaj pojawi się pytanie − skąd uczeń wie, że |AC| > 11.0 i szczerze mówiąc, nie
widzę sposobu jak uczeń liceum uargumentuje ten wybór.
Wskaż gdzie uczeń ma PEWNOŚĆ, że podana wartość (|AC| = 12 czy chociażby |AC| = 11.5) nie
będzie poza przedziałem.
6 cze 13:22

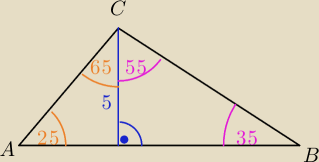
 Niby gdzie masz podane, że masz obliczyć korzystając z kątów 30,45,60
Niby gdzie masz podane, że masz obliczyć korzystając z kątów 30,45,60 

