Rozważ 9-wierzchołkowy, prosty i spójny graf, który ma dokładnie 12 krawędzi
Ania: 7. (a) Rozważ 9−wierzchołkowy, prosty i spójny graf, który ma dokładnie 12 krawędzi i 3 cykle.
Narysuj ten graf lub wyjaśnij dlaczego taki graf nie istnieje. (b) Ukorzenione drzewo jest to
drzewo z wyróżnionym wierzchołkiem zwanym korzeniem. Narysuj wszystkie ukorzenione drzewa,
które mają 5 wierzchołków. Wskaż, które z nich są izomorficzne?
5 cze 16:51
Bleee:
I problem polega na

5 cze 17:19
Ania: Zawsze mi wychodzi 11 krawedzi
5 cze 17:42
Ania: ma ktoś pomysł ? Wychodzi mi ze w a) taki graf nie istnieje, ale nie wiem jak to udowodnic
5 cze 18:31
Bleee:
A możesz narysować ten graf o 11 wierzchołkach i zaznaczyć te 3 cykle?
5 cze 18:37
Ania:
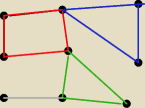
5 cze 18:40
Bleee:
Co prawda robię to w głowie, ale mi się wydaje że z 11 wierzchołkami masz 2 cykle, a z 12 będą
właśnie 3 cykle
5 cze 18:41
Ania: ma byc 9 wierzchołków a 12 krawedzi
5 cze 18:42
Ania: ktoś coś ?
5 cze 19:38
Bleee:
Okey... Ja myślałem tylko o pełnych cyklach i tylko je rozpatrywanem jako cykle.
5 cze 19:40
Bleee:
To teraz trzeba to udowodnić.
Zauważ że spójny, prosty graf nie posiadający żadnych cykli ma n−1 krawędzi. Każda następna
krawędź będzie tworzyć przynajmniej jeden cykl. Tak więc, przy n+3 krawędziach będziemy mieli
conajmniej 4 cykle.
5 cze 19:48
Ania: oki dzieki za pomoc
a pkt b) ? Ogolnie narysowalam 5 drzew ale nie wiem które są izomorficzne, wie ktoś jak to
zrobic ?
5 cze 20:05
Ania:
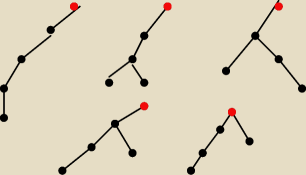
5 cze 20:10
wredulus_pospolitus:
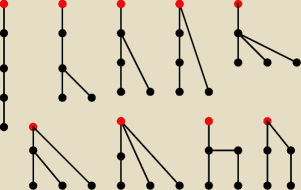
i to nie są wszystkie
5 cze 20:36
wredulus_pospolitus:

Jeszcze masz ten
ale jeden z tamtych wypada (nr 8 bo to nic innego jak nr 3)
5 cze 20:37



 i to nie są wszystkie
i to nie są wszystkie
 Jeszcze masz ten
ale jeden z tamtych wypada (nr 8 bo to nic innego jak nr 3)
Jeszcze masz ten
ale jeden z tamtych wypada (nr 8 bo to nic innego jak nr 3)