geometria analityczna kox72: Dwa boki równoległoboku zawierają się w prostych: x – y + 1 = 0 oraz 3x + 2y – 12 = 0. Punkt P(6, 4) jest punktem przecięcia się przekątnych równoległoboku. Wyznacz: a) równanie prostej zawierającej jeden z dwóch pozostałych boków równoległoboku b) współrzędne wierzchołków równoległoboku c) pole równoległoboku.

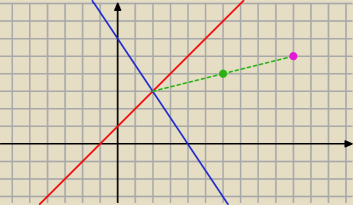
wredulus_pospolitus: 1) przecięcie prostych = jeden z wierzchołków 2) w równoległoboku przekątne przecinają się w połowie 3) rysujesz odcinek pomiędzy znanym wierzchołkiem a punktem P 4) a następnie go przedłużasz ... w ten sposób znajdujesz drugi wierzchołek 5) teraz wystarczy wyznaczyć proste równoległe do podanych prostych, przechodzące przez wyznaczony drugi wierzchołek Kooooniec

kox72: dzieki