funkcja maryska:

	2x
zbadaj monotoniczność funkcji f o wzorze f(x) =
	x+1

x+1 w zbiorze x=(0,∞) x₁ < x₂ doprowadziłam do postaci

2(x1−x2)
	licznik wychodzi na minusie mianownik na plusie
(x1+1)(x2+1)

czyli x₁ < x₂ ⇒ f(x₁)<f(x₂) czyli malejąca pytanie dobrze to mam ?

wredulus_pospolitus: No nie bardzo pokaż swoje obliczenia to pokażemy Ci gdzie masz błąd

Odys:

	2x
To jest wykres y=
	x+1

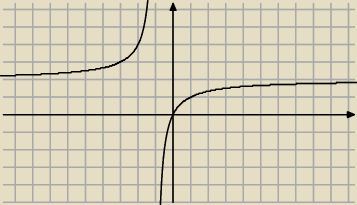
wiec chyba nie tak

wredulus_pospolitus: dodatkowo, można inaczej zapisać samą funkcję:

	2x		2(x+1) −2		2
f(x) =		=		= 2 −
	x+1		x+1		x+1

no i na dokładkę, zawsze można sprawdzić swój rezultat:

	18
f(9) =		= 1.8
	10

	198
f(99) =		= 1.98
	100

I widać od razu, że jednak ta funkcja nie może być malejąca w całym przedziale

Jerzy: Pochodna jest stale dodatnia,czyli funkcja stale rośnie w przedziałach.

maryska: pokazuje samo obleczenie

2x1		2x2		2x1(x2+1)−2x2(x1+1)
	−		=		=
x1+1		x2+1		(x1+1)(x2+1)

2x1x2+2x1−2x1x2−2x2
	=
x1+1)(x2+1)

2x1−2x2
	=
(x1+1)(x2+1)

2(x1−x2)
	licznik na minusie a mianownik na plusie tak jak pisałam
(x1+1)(x2+1)

wczesniej proszę o popraweco źle robie

Jerzy: Dlaczego twierdzisz,że mianownik jest stale dodatni ?

Odys: Zbadalas roznowartosciowosc a nie monotonicznosc

Bleee: Policzylas f(x₁) − f(x₂)

Bleee: Wiec błąd jest już na samiutkim poczatku

Bleee: Jerzy.... mianownik stałe dodatni że względu na przedział w którym bada monotonicznosc

maryska: mam zbadac monotoniczność w zbiorze zbiorze liczb R dodatnich czyli (0,∞) moze źle to rozumiem ? po drugie w szkole badamy monotonicznosć w ten sposób że piszemy x₁,x₂ itd potem patrzymy co po redukcji wychodzi różnowartowość nie miałam tego jeszcze

maryska: Bleee; ? o co pytasz ?

Odys: czyli f(x₁)−f(x₂)<0 funkcja rosnaca

maryska: Jerzy tak własnie jest badam w zbiorze R dodatnich wiec wydaje mis ie logiczne ze mianownik dodatni,

maryska: o rzesz OCZYWISCIE ROSNĄCA ! jaka slepota zamykamy, dzięki Odys

Bleee: Ja nie pytam... Ja stwierdzam że policzylas f(x₁) − f(x₂) =..... I wyszło Ci że ów różnica jest mniejsza od zera (prawidłowo), jednak wyciagasz z tego zły wniosek. Domyślnie przy monotonicznosc liczymy różnice f(x₂) − f(x₁) gdzie x₂ > x₁

maryska: pytałeś o mianownik i Jerzy ci to wyjasnił według mnie mianownik musi byc dodatni

maryska: wiem ze liczymy f(x₁)−f(x₂) ale porosili o moje obliczenia i tylko je skrotowo podalam choc oczywiscie sam zapis na sprawdzianie by nie przeszedl −to wiem

Bleee: Nie ja tylko Jerzy się pytał o mianownik Nie istotne. Widzisz już błąd w swoim rozumowania i to najważniejsze. Miej (na przyszłość) na uwadze to co napisane zostało o 13:11