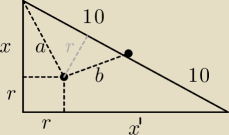
trójkat Igor: W trójkącie ABC o przeciwprostokątnej 20 kąt BOS=90⁰ gdzie O jest środkiem okręgu wpisanego w ten trójkąt,a S środkiem okręgu opisanego na tym trójkącie. Oblicz długości przyprostokątnych

wredulus_pospolitus: 1) Skoro przeciwprostokątna = 20 to promień okręgu opisanego na trójkącie prostokątnym = 10 2) z podobieństwa trójkątów:

x		a		r
	=		=
a		10		b

3) z tw. Pitagorasa: a² = r² + (10−c)² a² + b² = 10² b² = r² + c² (x+r)² + (x' + r)² = 20² no i masz układ 6 równań z 6−cioma niewiadomymi ... powodzenia

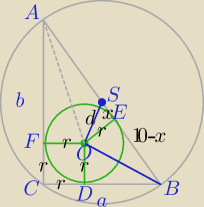Mila: |AB|=20 R=10 1) Tw. Eulera (geometria) d²=R*(R−2r) d²=10*(10−2r) W ΔOES: ( *) d²=r²+x² w ΔSOB: (**) r²=x*(10−x)⇔ r²=10x−x² podstawiamy do (*) 100−20r=10x−x²+x² 100−20r=10x x=10−2r⇔10−x=2r, 10−2r>0 i r>0⇔r∊(0,5) Podstawiamy do (**) r²=2r*(10−2r) r²=20r−4r² 5r²−20r=0 5r*(r−4)=0 r=4 2) w Δprostokątnym ABC : a²+b²=c² a+b=2r+2R −−−−−−−−−−−−−− a²+b²=400 a+b=8+20, a+b=28 b=28−a a²+(28−a)=400 a=12, b=16 lub a=16, b=12 Teraz ustal, którą masz dać odpowiedź (|∡SOB|=90^o)