rachunek prawdopodobieństwa Piotr: w jaki sposób obliczyć to zadanie? 2 Badania statystyczne przeprowadzone wśród studentów wykazały, że: 50% czyta dziennik A, 60% czyta dziennik B, 50% czyta dziennik C, 20% czyta dzienniki A i B, 30% czyta dzienniki B i C, 30% czyta dzienniki A i C, 10% czyta wszystkie dzienniki. Wyznacz prawdopodobieństwo, że przypadkowo wybrany student: a) czyta dziennik A, jeżeli wiadomo, że nie czyta dziennika B, b) czyta dziennik A, jeżeli wiadomo, że czyta co najmniej dwa dzienniki.

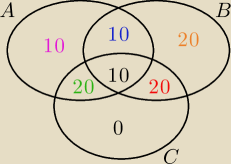
xyz: 50% czyta A 60% czyta B 50% czyta C 20% czyta A i B 30% czyta B i C 30% czyta A i C 10% czyta wszystkie zaczynasz od rysunku (mamy 3 dzienniki A,B i C zatem rysujemy 3 zbiory i wszystkie mozliwe przeciecia w tych zbiorach) Informacje w zbiorach zapisze w %. Czyli zaczynamy od tego co na pewno wiadomo (najbardziej szczegolowe info) czyli od tego, ze 10% czyta wszystkie) teraz od tych co maja troche mniej szczegolowe, ale nadal szczegolowe (xD) czyli od: 20% czyta A i B No to skoro w polaczeniu zbiorow (czesc wspolna) A i B mamy juz 10%, to uzupelniamy kolejnymi 10 aby uzyskac lacznie 20 30% czyta B i C Patrzymy na czesc wspolna B i C, widzimy ze mamy te 10% juz to brakuje jeszcze 20, wiec wpisujemy 30% czyta A i C czesc wspolna A i C wynosi poki co 10, wiec brakuje 20 No i teraz koncowka rozpisania 50% czyta A No to patrzymy na zbior A, jest tam poki co 20 + 10 + 10 = 40 zatem brakuje 10, to wpisujemy 10 (co oznacza ze 10% czyta TYLKO A) 60% czyta B no to znowu sumujemy zbior B poki co mamy 10 + 10 + 20 = 40 brakuje 20 (co oznacza ze 20% czyta tylko B) 50% czyta C poki co mamy 20+10+20 = 50, zatem wpisujemy 0 w czesci tylko C

xyz: odczytanie info do a) i b) z rys. nie powinno byc trudne

Piotr: Dziękuję bardzo za szczegółowe wyjaśnienie! Z tego co widzę, w obu przypadkach będzie to 30. Jeszcze raz wielkie dzięki!