okrąg opisany na trójkącie A: Wysokość opuszczona z wierzchołka C kąta prostego trójkąta ABC dzieli jego przeciwprostokątną na odcinki AD i DB o długościach odpowiednio 3 i 4. Oblicz promienie okręgów opisanych na trójkątach ABC, ADC i DBC

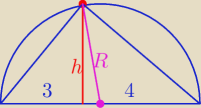
janek191: h² = 4*3 h = 2√3

	7
R =		= 3,5
	2

P1		0,5*4*2√3		4
	=		=		= k2
P		0,5*7*2√3		7

	2
k =
	√7

	2
R1 = k*R =		*3,5 = √7
	√7

P2		0,5*3*2√3		3
	=		=		= s2
P		0,5*7*2√3		7

	√3
s =
	√7

	√3		√21
R2 = s*R =		*3,5 =
	√7		2

A: dziękuję!