pomocy ewa: W trójkąt wpisano okrąg o promieniu 1cm. punkt styczności okręgu z jednym z boków dzieli bok na części o długościach 2cm i 3cm.Oblicz pole trójkąta

ite:

	r
P=(2+3+3+x+x+2)*
	2

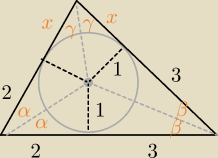
2α + 2β + 2γ = 180^o α + β + γ = 90^o

	1		1
tg γ =		⇒ x =
	x		tg γ

stosujemy wzory redukcyjne:

	ctg α*ctg β − 1
tg γ = tg(90o−α−β) = ctg(α+β) =
	ctg α + ctg β

ewa: i co dalej? wynik ma być 6

iteRacj@: Taki będzie wynik. Teraz tylko trzeba do ostatniego równania podstawić wartości ctg α i ctg β odczytane z rysunku. Znając wartość tg γ, obliczysz x a potem pole trójkąta.

ewa: super dziękuję bardzo wszystko pasuje

Eta: 2 sposób

	1
P=rp i P=		*5*(2+x)*sin(2α)
	2

P=x+5 i sinα=1/√5 i cosα=2/√5 to sin(2α)=2sinα*cosα =... =4/5

	1		4
P=		*5*(2+x)*		⇒ P=4+2x
	2		5

zatem 4+2x=x+5 ⇒ x=1 to P=x+5 = 6