nie umiem ewa: oblicz pole trójkąta wpisanego w okrąg o promieniu R (środek okręgu leży poza Δ) i dwóch bokach długości R i R(√2−√3)

daras: https://www.zadania.info/d1351/5782419

ewa: nijak ma się ten link do mojego zadania, to wogóle inny trójkąt

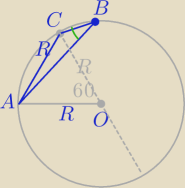
Mila: |BC|=R*√2−√3 Kąt środkowy: |∡AOC|=60^o |∡CBA|=30⁰ jako kąt wpisany oparty na łuku AC, Z tw. sinusów:

BC
	=2R
sinA

R*√2−√3
	=2R
sinA

	√2−√3		√2+√3
sinA=		, cosA=
	2		2

	√2−√3		√2+√3
2*sinA*cosA=2*		*
	2		2

	1
sin2A=		⇔2A=30o
	2

|∡A|=15^o |∡C|=180−(30+15)=135^o

	1		√2
PΔ=		R*R*√2−√3*
	2		2

P_Δ= dokończ

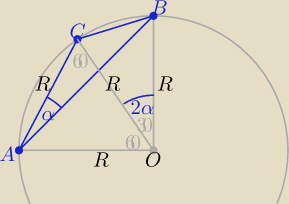Eta: Można też dokończyć tak: skoro |∡CAB|=30^o to ΔAOB prostokątny równoramienny

	R2√3		1		1		1
P(ABC)=P(AOBC)−P(AOB)=		+		R*R*		−		R2
	4		2		2		2

	R2
P(ABC)=		(√3−1)
	4

==================

Eta: Poprawiam zapis skoro |∡COB|=30^o

daras: a teraz ma się jak, może chociaż dziękuję ewuś

ewa: ale tobie daras nie mam za co dziękować. bardzo bardzo dziękuję Eta i Mila to ma sens

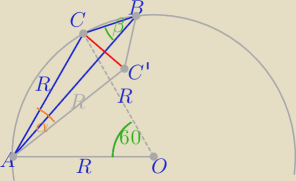Mila: |BC|=R√2−√3 1) β=30^o jako kąt wpisany w okrąg oparty na tym samym łuku co kąt środkowy AOC 2) C'− punkt symetryczny do punktu C względem AB ΔCC'B− Δrównoboczny o boku R*√2−√3 3) W ΔCC'A: ( R*√2−√3)²=R²+R²−2*R*R *cosα , R²*(2−√3)=2R²−2R²*cosα⇔ 2−√3=2−2cosα

	√3
cosα=
	2

α=30^o |∡CAB|=15^o 4)

	1
PΔABC=		*R*R*√2−√3*sin(180−45)
	2

	R2		√2		R2
PΔABC=		*√2−√3*		=		*√4−2√3=
	2		2		4

	R2
=		(√3−1)
	4

=================

Eta: Hej Mila Ja nie kwestionowałam Twojego rozwiązania !

Mila: Wiem doskonale i podoba mi się Twoje dokończenie

daras: l'art pour l'art