Narysuj logarytm
Tomek : Wykreśl funkcje postaci f(x) = log o podstawie (x+2) z liczby logarytmowanej (x+4).
Rozumiem tyle ze trzeba rozpatrzyć dwa przypadki kiedy to funkcja będzie rosnąca czyli x>−1
I kiedy funkcja jest malejąca czyli x€(−2; −1) ale nie zgadza mi się dziedzina. Czy mógłby ktoś
to narysować krok po kroku? Dziękuje 🙂
27 maj 01:46
6latek: Panie , a dlaczego dwa przypadki ? Przeciez to nie jest nierownosc .
Okreslasz dziedzine Potem np robisz tabelke i rysujesz wykres
27 maj 08:00
przypadki są potrzebne:
logx+2(x+4)
zał. x+4>0, x+2≠1, x+2>0 → x∊(−2,−1)U(−1,∞)
27 maj 08:28
6latek: Ale przeciez mozemy zapisac to inaczej x∊(−2,
∞)\(−1)
Ale przedszkolak moze sie mylic oczywiscie

27 maj 08:32
przypadki są potrzebne czasem:
teraz policz granice na krańcach dziedziny, asymptoty, itd. czyli badanie przebiegu zmienności
funkcji
27 maj 08:32
przypadki są potrzebne czasem: tabelka tutaj to za mało : (
27 maj 08:33
przypadki są potrzebne czasem:
Można tak oczywiście zapisać: x∊(−2,∞)\(−1), ale nadal nie wiemy, jakie wartości przyjmuje
funkcja dla argumentów bliskich −1. A narysować trzeba.
27 maj 08:35
6latek: Dla (−1) narysowalbym na wykresie (o)
Pewnie masz racje ze nalezy zbadac przebieg zmiennosci funkcji (ale dlaczego tego nie napisal?)
27 maj 08:39
piotr: mamy takie granice na krańcach dziedziny:
limx→−2+ f(x) = 0
limx→−1− f(x) = −∞
limx→−1+ f(x) = +∞
limx→+∞ f(x) = 1
oraz:
f(0) = 2
27 maj 09:00
piotr: czyli asymptota pionowa x = −1
oraz asymptota pozioma y = 1
27 maj 09:02
przypadki:
@6−latku 8:39 Mamy polecenie "wykreśl", ale sposób rozwiązania nie musi być podany w zadaniu,
trzeba samemu zdecydować, czy zbadać przebieg zmienności.
8:00 Nie można się oprzeć na znajomości wykresu h(x)=logax, ponieważ podana funkcja nie jest
f.logarytmiczną.
h(x)=logstała(x+4) byłaby nią, ale f(x)=logx+2(x+4) już nie.
27 maj 10:58
6latek: Rozumiem .
27 maj 14:33
Tomek : Dziekuje za takie zaangażowanie. Może znajdzie się osoba która narysowalaby ta funkcje w
oparciu o te asymptoty?
Na podstawie wykresu muszę rozwiązać nierówność f(x)<2.
27 maj 15:22
piotr:
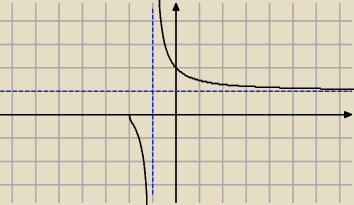
27 maj 15:31

