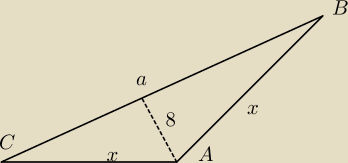
Planimetria ktoś: Wysokość AD opuszczona na podstawę BC trójkąta rozwartokątnego równoramiennego ABC (AB=AC) ma długość 8 cm a promień okręgu opisanego na tym trójkącie 13 cm. a)pole trójkąta jest równe... b)długość ramienia AC... c)promień okręgu wpisanego w tym trójkąt... Proszę o pomoc. Nie wiem nawet jak zacząć.

Bleee: Jaka jest zależność pomiedzy promienie okręgu opisanego a bokiem i przeciwlegly kątem? Wyznaczasz kąty, Wyznaczasz wysokość, AC przecież masz podane w treści zadania Jaka jest zależność pomiedzy bokami trójkąta a promienie okręgu wpisanego w trójkąt?

ktoś: Dalej nie za bardzo rozumiem. Czy mógłbyś wyjaśnić to bardziej "łopatologicznie"?

Bleee: Lopatologicznie − − − (1) sprawdź w książce wzór na obliczenie promienia okręgu opisanego na trójkącie. (4) Znajdź wzór na obliczenie promienia okręgu wpisanego w trójkąt. (2) Znajdź tabelkę trygonometryczna. (3) Znajdz wzór na pole trójkąta. Masz łopatologicznie.

ktoś: Żeby było jasne, wzór na promień okręgu opisanego na trójkącie to: R=²₃h, wzór na obliczenie promienia okręgu wpisanego w trójkąt: r=^P_p ?

wredulus_pospolitus:

	2
R =		h <−−−− BZDUUUURA Ten wzór się tyczy tylko i wyłącznie trójkąta równobocznego.
	3

ktoś: R=^abc_4P Czy ten wzór jest dobry?

wredulus_pospolitus:

	a*x*x		ax2		x2
R = 13 =		=		=		−> x =
	4P		a*8   4   2		16

a = 2*√x² − 8² = P =

	2P
r =		= ...
	a+x+x

ktoś: Mam problem z policzeniem x. Możesz pomóc?

wredulus_pospolitus:

	x2
13 =		masz problem aby tutaj wyznaczyć x
	16

ktoś: Dobra, nie zwróciłem uwagi na tą 13. x=4√13 ?

wredulus_pospolitus: tak

ktoś: a=24 P=26,42 r=~~0,99 ?

wredulus_pospolitus:

	24*8
P =		=
	2

ktoś: P=98 r=3,6?

wredulus_pospolitus: podajemy DOKŁADNE wartości więc r ≠ 3,6 Co wy macie z tym wbijaniem pierwiastków do kalkulatora? Pamiętaj o wyciągnięciu niewymierności z mianownika

ktoś: r=^{1321√13 − 3963}₈₀₀ ?

wredulus_pospolitus:

	96		49		49(4√13−12)
r =		=		=		=
	24 + 8√13		12 + 4√13		208 − 144

	49*4(√13 − 3)		49(√13 − 3)
=		=
	4*16		16

nie mam bladego pojęcia skąd masz te liczby

ktoś: Wielkie dzięki za pomoc. Teraz nareszcie to rozumiem.