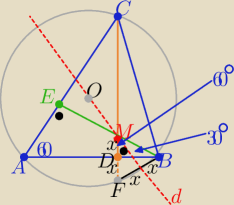
 1/ rysunek zgodny z treścią zadania
punkt M −− ortocentrum trójkąta ABC
2/ trójkąt BMF −−− równoboczny o boku 2x
kąt BMD=60o to dwusieczna jest symetralną cięciwy BF
zatem przechodzi przez środek O okręgu opisanego na tym trójkącie
co kończy dowód
1/ rysunek zgodny z treścią zadania
punkt M −− ortocentrum trójkąta ABC
2/ trójkąt BMF −−− równoboczny o boku 2x
kąt BMD=60o to dwusieczna jest symetralną cięciwy BF
zatem przechodzi przez środek O okręgu opisanego na tym trójkącie
co kończy dowód