Okrag wpisany w trojkat ......: Wyznacz równanie okręgu wpisanego w trójkąt o wierzchołkach A(−6,−2) B(4,−6) C(−2,4). Wyznaczalam równania prostych zawierające te boki l_AB: 2x+5y+22=0, l_BC: 5x+3y−2=0, l_AC: 3x−2y+14=0. Wiem że trzeba liczy dwusieczne kątów między tymi prostymi że wzoru na odległość punktu P(x,y) od prostych i przyrównać je ale po rozpisaniu wartości bezwzględnej powstają 2 równania i nie wiem które wybrać do dalszych obliczeń?

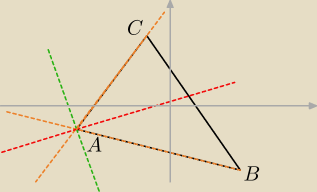
iteRacj@: Proste AC i AB wyznaczają dwa kąty (ostry i rozwarty). Prosta zawierająca dwusieczną ostrego jest zaznaczona na czerwono, dwusieczną rozwartego na zielono. <CAB (kąt trójkąta w który wpisano okrąg) jest kątem ostrym. Na podstawie rysunku do zadania wykonanego w układzie współrzędnych widać, do której z nich należy środek szukanego okręgu.

Mila: Sprawdź, czy dobrze przepisałaś współrzędne punktów

......: Dobrze przepisalam, wyniki wychodza bardzo dziwne i jest dużo pierwiastków, jest inny sposób żeby wybrać odpowiednią dwusieczna bez rysunku?

Mila: Też mam skomplikowane wyniki. Obliczyłam promień z wzoru na pole Δ.

iteRacj@: Milu podpowiesz jakiś prosty sposób wybrania dwusiecznej? Ja widzę tylko sprawdzenie, czy wybrana dwusieczna ma pkt wspólny z trzecim bokiem (tu BC). Nie jest to szybkie.

Mila: 1) Normalizuję AB^→i AC^→ 2) Suma wektorów daje wektor kierunkowy dwusiecznej poprowadzonej z A. Tu rachunki są nieprzyjazne. Chyba są inne wsp. jednego z wierzchołków.

......: Wierzchołki niestety nie są pomylone dlatego wszystko się komplikuje

Mila: Z jakiej książki masz to zadanie?

iteRacj@: dzięki Mila za odpowiedź z 22:26

Mila:

......: To nie jest z książki, wymyślone z głowy ale nie przeze mnie

Mila: To powiedz autorowi, aby sam to policzył. Mogę podać treść zadania, abyś mogła rozwiązać podobne zadanie.

Mariusz: A(−6,−2) B(4,−6) C(−2,4). a = BC = √(−2−4)²+(4−(−6))² = 2√34 b = AC = √(−2−(−6))²+(4−(−2))² = 2√13 c = AB = √(4−(−6))²+(−6−(−2))²=2√29 (a+b+c)(−a+b+c)(a−b+c)(a+b−c) (a+b+c)(−a+b+c) ((b+c)+a)((b+c)−a)=(b²+2bc+c²−a²) (a−b+c)(a+b−c) (a−(b−c))(a+(b−c))=(a²−(b²−2bc+c²))=(a²−b²−c²+2bc) (b²+2bc+c²−a²)(a²−b²−c²+2bc) ((b+c)²−a²)(a²−(b−c)²) a²(b+c)²−(b−c)²(b+c)²−a⁴+a²(b−c)² a²(b²+2ab+c²+b²−2bc+c²)−(b²−c²)²−a⁴ a²(2b²+2c²)−(b⁴−2b²c²+c⁴)−a⁴ 2a²b²+2a²c²+2b²c²−a⁴−b⁴−c⁴ P=√2*34*13+2*34*29+2*13*29−1156−169−841 P=√884+1972+754−1156−169−841 P=√3610−2166=√1444=38

	38
r=
	√34+√13+√29

A(−6,−2) B(4,−6) C(−2,4). 2√34(−6−xS)+2√13(4−xS)+2√29(−2−xS)=0 2√34(−2−yS)+2√13(−6−yS)+2√29(4−yS)=0 −2(√34+√13+√29)xS−12√34+8√13−4√29=0 −2(√34+√13+√29)yS−4√34−12√13+8√29=0

	−6√34+4√13−2√29
xS=
	√34+√13+√29

	−2√34−6√13+4√29
yS=
	√34+√13+√29

	−6√34+4√13−2√29
(x −		)2+
	√34+√13+√29

	−2√34−6√13+4√29		38
(y−		)2=(		)2
	√34+√13+√29		√34+√13+√29

Można jeszcze bawić się w usuwanie niewymierności z mianownika Na równanie okręgu opisanego jest wzór z wyznacznikami

Mariusz: Konstrukcja https://www.geogebra.org/classic/q8bkd5en

Mila: 1) Pole Δ i promień okręgu wpisanego w Δ: A(−6,−2), B(4,−6), C(−2,4) AB^→=[10, −4], |AB|=√116=2√29 AC^→=[4, 6], |AC|=√52=2√13 BC^→=[−6,10], |BC|=√136=2√34

	1		1		1
PΔ=		|W|=		*|10*6+4*4|=		*76=38
	2		2		2

38=(√13+√29+√34)*r

	38
r=
	(√13+√29+√34)

================== 2) Dwie dwusieczne

Mariusz: I co dalej z tymi dwusiecznymi

Mila: Jak liczysz (x_s,y_s) ? Podoba mi się sposób, ale skąd taki wzór?

Mila: 22:26 podałam jak wyznaczyć wektory kierunkowe dwusiecznych, ale nie chce mi się liczyć . Może będę miała ochotę, to policzę, ale nie dzisiaj

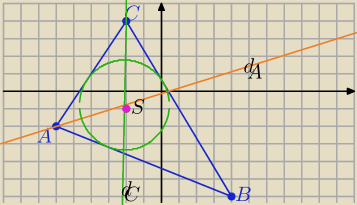
Mila: S≈(−2.11,−0.79)

wredulus_pospolitus: ale nie trzeba z dwusiecznych ... jak już mamy promień (który niestety jest brzydki) to wystarczy: 1) Zrobić prosta równoległą do (powiedzmy) AC oddaloną o promień 2) Zrobić drugą prostą równoległą (powiedzmy do AB) 3) Przecięcie prostych będzie naszym środkiem okręgu

wredulus_pospolitus: i chyba właśnie tak Mariusz zrobił

Mariusz: W tablicach znalazłem równanie wektorowe wyznaczające środek okręgu wpisanego aPA + bPB + cPC = 0 gdzie P to środek okręgu wpisanego A,B,C to wierzchołki o danych współrzędnych a długość boku naprzeciw wierzchołka A b długość boku naprzeciw wierzchołka B c długość boku naprzeciw wierzchołka C Jak wyprowadzić to równanie wektorowe to już wam pozostawiam

Mila: Dziękuję Mariusz

jc: Piękny i prosty wzór. Dwusieczna przechodząca przez A przecina odcinek BC w punkcie D i przy okazji dzieli trójkąt ABC na dwa trójkąty, stosunek pól tych trójkątów = b:c = CD : BD.

	b		c
Stąd D=		B +		C.
	b+c		b+c

	a		b		c		a		b+c
S=		A +		B+		C =		A +		D.
	a+b+c		a+b+c		a+b+c		a+b+c		a+b+c

Wniosek. S leży na dwusiecznej AD. Podobnie widzimy, że S leży na pozostałych dwóch dwusiecznych, a więc jest środkiem okręgu wpisanego.

jc: Też bardzo dziękuję, za takk śliczny wzór

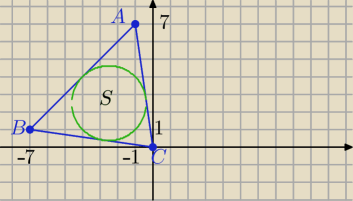
Mila: Zadanie dla uczniów II klasy LO. A=(−1,7), B=(−7,1), C=(0,0) Szukane : środek okręgu wpisanego w ΔABC, promień okręgu.

	5		5
S=(−		,		) − środek okręgu wpisanego w ΔABC.− obliczone wg wzoru z 23:31
	2		2

	3
r=		− obliczone z odległości S od boku AC.
	√2