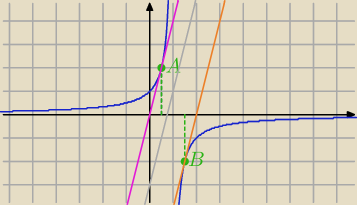
Pochodne Uczeń : Funkcja określona wzorem 1 / 1− x do wykresu funkcji f można poprowadzić w punktach A i B dwie styczne, które są równolegle do prostej o rownaniu y = 4x −3 Oblicz współrzędne A i B wiedząc, że x_a < x_b oraz napisz rownanie stycznej w punkcie A do wykresu funkcji f Nie wiem od czego zacząć

Jerzy: Od wyznaczenia punktów sptyczności.

hary: po co te igrek czymu nie y

Jerzy: @hary ..... nie wiem co bierzesz,ale bierz po pół.

Uczeń : Aby wyznaczyć punkt styczności muszę porównać rownanie prostej i pochodną w/e funkcji?

jc: 1/1 − x = 1 − x, czy na pewno o to Ci chodziło?

Uczeń : 1/(1−x)

jc: f(x)=1/(1−x) f'(x)=1/(1−x)²=4, x=1/2 lub x= 3/2 f(1/2)=2, y=4x+2 f(3/2)=−2, y=4x−2

Uczeń : Skąd to x=1/2 lub x=3/2?

Uczeń : Tzn. Skąd ta 4 w rownaniu : p

Jerzy: Bo f’(x) musi być równe 4 ( współczynnik kierunkowy stycznej )

Mila:

	1
f(x)=
	1−x

1) równanie stycznej : s: y=f'(x₎)*(x−x₀)+f(x₀) f'(x₀)=4 z treści zadania (styczne, są równolegle do prostej o równaniu y = 4x −3) s: y=4x+b − równanie stycznej. 2) Nie znamy punktów styczności A i B A=(x₀,y₀) f'(x₀)=4

	1
f'(x)=
	(1−x0)2

1
	=4 ⇔ 1=4(1−x0)2
(1−x0)2

	1
(1−x0)2=
	4

	1		1
1−x0=		lub 1−x0=−
	2		2

	1		3
x0=		lub x0=
	2		2

1		3
	<
2		2

	1		1
f(		)=		=2 =y0
	2		1   1−   2

	1
Mamy jeden punkt styczności : A= (		,2)
	2

	3		1
f(		)=		=−2
	2		3   1−   2

	3
B=(		,−2)− drugi punkt styczności
	2

3) styczne : s_a:

	1
2=4*		+b⇔b=0
	2

y=4x s_b:

	3
−2=4*		+b⇔b=−8
	2

s_b: y=4x−8 ================

jc: Nie wiem skąd wziąłem styczne , ale punkty A i B były ok.

Uczeń : Dzięki Mila, świetnie wyjaśnione

Mila: