optymalizacja, f.kwadratowa
kuba:
Dany jest trójkąt ABC w który wpisano okrąg
Styczna EF do tego okręgu jest równoległa do boku BC
Wyznacz największą długość odcinka EF tej stycznej wiedząc że obwód trójkąta ABC
jest równy 2p
22 maj 22:18
Maciess: styczna moze zawierac bok BC?
22 maj 22:23
kuba:
Zapomniałem dopisać ( tak mam na rysunku)
że punkty E i F są punktami przecięcia stycznej z bokami AB i AC
22 maj 22:29
jc: p/8 ?
22 maj 23:36
jc:
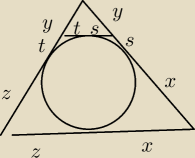
(y−t):(y+z) = (y−s):(y+x) = (s+t):(z+x)
(y−t)(z+x)=(y+z)(s+t)
(y−s)(z+x)=(y+x)(s+t)
dodajemy przyjmując, że m=s+t, p=x+y+z
(y−m)(p−y)=(p+y)m
2pm = y(p−y) ≤p
2/4 (największa wartość)
m≤p/8, największa wartość m=p/8
22 maj 23:42
Eta:
A mnie wyszło m=p/4
22 maj 23:57
jc: Zgubiłem 2.
(2y−m)(p−y)=(y+p)m
m=p/4
23 maj 00:10
Eta:
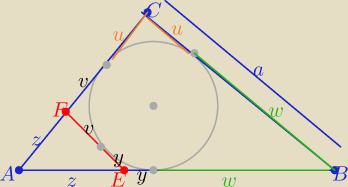
2w+2u=2a
to
Obwód ABC=2p Obwód AEF= 2p−2a
|EF|=x
z podobieństwa trójkątów AEF i ABC z cechy (kkk)
| x | | 2p−2a | | x | | a | |
| = |
| ⇒ |
| =1− |
| |
| a | | 2p | | a | | p | |
| | 1 | |
x=− |
| a2+a −− parabola ramionami do dołu |
| | p | |
| | 1 | | p2 | | p | |
to xmax= − |
| * |
| + |
| |
| | p | | 4 | | 2 | |
===========
23 maj 00:14
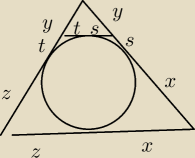 (y−t):(y+z) = (y−s):(y+x) = (s+t):(z+x)
(y−t)(z+x)=(y+z)(s+t)
(y−s)(z+x)=(y+x)(s+t)
dodajemy przyjmując, że m=s+t, p=x+y+z
(y−m)(p−y)=(p+y)m
2pm = y(p−y) ≤p2/4 (największa wartość)
m≤p/8, największa wartość m=p/8
(y−t):(y+z) = (y−s):(y+x) = (s+t):(z+x)
(y−t)(z+x)=(y+z)(s+t)
(y−s)(z+x)=(y+x)(s+t)
dodajemy przyjmując, że m=s+t, p=x+y+z
(y−m)(p−y)=(p+y)m
2pm = y(p−y) ≤p2/4 (największa wartość)
m≤p/8, największa wartość m=p/8
 2w+2u=2a
to
Obwód ABC=2p Obwód AEF= 2p−2a
|EF|=x
z podobieństwa trójkątów AEF i ABC z cechy (kkk)
2w+2u=2a
to
Obwód ABC=2p Obwód AEF= 2p−2a
|EF|=x
z podobieństwa trójkątów AEF i ABC z cechy (kkk)