objętość Maciess: Obliczyć objętość bryły powstałej w wyniku obrotu krzywej dookoła osi OX tej części która jest nad osią OX x²+y²−6y−16=0 To zadanie ze studiow. Da rade to zrobić bez całek? x²+(y−3)²=25 ⇒S=(0,3) r=5 Nie wiem jak u mnie z wyobraźnią przestrzenną, ale po obrocie to otrzymamy dwie jednakowe części kul (nad i pod osia OX).

	500
Więc licząc objętość całej kuli V=		π i teraz jak jakos sprytnie okresle "ile zostało u
	3

góry" to będzie poprawnie?

jc: Jak obracasz dookoła, to będziesz miał kulę o promieniu 5 i objętości V (jak powyżej). To wszystko.

azeta: nie do końca. tak by było gdyby środek tego okręgu znajdował się dokładnie w środku układu współrzędnych. u Ciebie ten srodek to (0,3) − a zatem powstała krzywa będzie obciętym okręgiem, a w konsekwencji obrotu bryła nie będzie kulą.

Maciess:

	3
cos(x)=
	5

	7
cos(2x)=2cos2(x)−1=−
	25

	7
arccos(−		)=106.3o (tutaj wujek wolfram musiał pomóc)
	25

	1063		500π		5315π
Objętość wyciętej częsci Vw=		*		=
	3600		3		108

Odejme od tego objętość stożka niebieskiego V_s=16π i rózowa część to

	5315π		5315π		1728π		3587π
Vr=		−16π=		−		=
	108		108		108		108

Więc objętość na osią OX to bedzie

	500π		5315π		18000π		5315π		14413π
Vk−Vr=		−		=		−		=
	3		108		108		108		108

Czy jest poprawnie?

jc: Widzę, że bzdurę napisałem.

jc: A gdyby użyć twierdzenia Goldena? Objętość = 2π * pole * (odl. śr masy od osi)

Maciess: Nie znam tego twierdzenia wiec nie wiem czy można go tutaj użyć. A co powiesz o moim rozwiązaniu? Czy jest metodycznie poprawne?

jc: Maciess, sprawdź, czy Twoje rozumowanie byłoby słuszne dla koła stycznego do osi obrotu. Wtedy powinno wyjść V=2π²R³.

Maciess: Nie wiem czy dobrze korzystam z tego twierdzenia, ale za kazdym razem wychodzi (przybliżony) wynik inny niz u mnie.

Maciess: Czyli trzeba czekać aż przyjdzie pan Mariusz i zrobi całkami

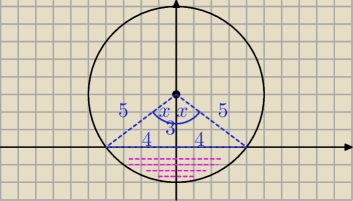
jc:

	2
R=5, a=3, T=		(R2−a2)3/2 = 128/3
	3

V=2π(T + a*P), P= pole obciętego koła.

jc: P=πR² − pole wycinka + pole trójkąta

Maciess: wiem, wiem

jc: pole trójkąta = 12 pozostaje pole wycinka = R² arctg 4/3 = 25*arctg 4/3 Podstawiasz i masz wynik.

Maciess: zjadłeś π

Maciess:

	2537π+1728
wyszło V=106 (znowu wujek wolfram) podstawiłem twoje T i pole wyszło mi
	144

Maciess: Jestem tylko ciekaw gdzie zrobiłem coś niepoprawnie matematycznie, bo rachunkowo raczej okej. Podejrzewam, ze źle policzyłem wycinek kuli.

Maciess: wziąłem z wikipedii wzór na wycinek kuli

	2		100π
V=		πR2h =
	3		3

	500π		52π		448π
Vnad OX=		−		=
	3		3		3

juz nie wiem co w koncu jest dobrze

jc: U mnie P jest polem wycinka koła, a nie objętością wycinka kuli.

jc: Jaki masz wynik dla koła stycznego do osi?

Maciess: robiłem twoim sposobem T wziąłem jakie mi podałes kąt 2x=106.3^o P=πR²−1063/3600πR²+12=πR²(1−1063/3600)+12=25PI(2537/3600)+12=U{2537PI}{14

	2537PI+1728
4}+12=
	144

	128		2537PI+1728
V=2π(		+3*		)
	3		144

https://www.wolframalpha.com/input/?i=2π(128%2F3%2B3*(2537PI%2B1728)%2F144) musiałem źle wklepac