Oblicz objętość brył ograniczonej powierzchniami Michał :): Dzień dobry! Mam gorącą prośbę o wsparcie mych działań w obliczaniu objętości brył ograniczonych pewnymi funkcjami jakoś nie mogę sobie poradzić i byłbym wdzięczny na nakierowanie mnie − jak znaleźć obszar całkowania bryły oraz z jakich całek go wyliczyć. a) na pierwszy ogień mamy takie ogarniczające powierzchnie: f(x)=x²+y²+z²=9 i g(x)=x²+y²=4 Z moich przemyślelń powstaje taki stożek z tej pierwszej funkcji który zaczyna się w 9 na osi z, natomiast druga funkcja to walec biegnacy od −oo do oo po osi z o promieniu 2. Problem w tym że nie wiem jaka powierzchnia ogranicza go z dołu w końcu biegnie od −oo do f(x). No nie wiem jak to zpisać jaki jest obszar całkowania i z jakiego obszaru mam to całkowanie wykonać. Ja bym stawiał że z=√9−x²−y² to jest obszar całkowania... chyba proszę o rozwiązanie choć tego etapu. Całkę sobie sam wyliczę (chyba ) b)x²+y²=z² x²+y²−2y=0 Tutaj też nie wiem mam taki sam stożek tylko tym razem w górę i zaczynający się w z=0 i ogranicza go do nieskończoności walec x²+y²−2y=0 którego promień obliczam tworząć wzór skróconego mnożenia x²−(y−1)²=1 To tyle dzięki z góry za poświecony mi czas =)

jc: (a) Sfera o promieniu 3 przebita centralnie rurą o promieniu 2. Powierzchnie dzielą przestrzeń na 5 obszarów. Który obszar Cię interesuje? (b) Stożek przebity rurą przylegającą do osi stożka. Powierzchnie dzielą przestrzeń na 6 obszarów. Tu jest o tyle łatwiej, że tylko jeden obszar ma skończoną objętość (w poprzednim zadaniu mieliśmy 2 takie obszary).

jc: (b) V=∫∫ 2√x²+y² dx dy, x²+y² ≤ 2x Przejdź do zmiennych biegunowych: x=r cos φ, y=r sin φ.

Michał :): jc wow wow to faktycznie przecież jest sfera.... ale ze mnie kretyn no to a) licze pole po tym gornym obszarze w środku rury i mnoże go razy dwa. Czyli: całke p{9−x²−y²)r po obszarze od o 0 do 2π po dφ i całke 0 do 2 dla dr? Czyli to będzie ta całka podwójna ∫∫(9−r²)r dr dφ A to b :X nie do końca rozumiem gdzie ten skończony obszar znajduje się w tej bryle. 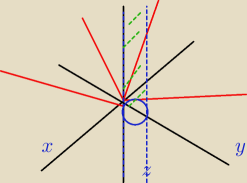i nie do końca rozumiem czemu V rozpisałes jako 2√x²+y² Narysowałęm rysunek... wiem że nie idealny ale ten zielony obszar to jest chyba ich część wspólna ? Tylko że chyba nieskończona...

jc: Górna część stożka: z=√x²+y², dolna część: z=−√x²+y², różnica = 2√x²+y². Pomyliłem literę: x²+y²≤2y, ale obszar ten i tak daje tą samą objętość.

Michał :): ym ale czemu dolna część to z=−√x²+y² tego nie rozumiem. I czemu robisz taki bajer że x²+y²≤2y tam faktycznie jest x²+y²=2y ale uzależniasz to od yka i jeszcze <= dajesz hmnnn tego etapu nie panimaju.

jc: x²+y²=2y określa linię, a nam chodzi o pewien obszar na płaszczyźnie, stąd nierówność. W ogóle należałoby opisać obszar nierównościami: x²+y² ≥ z², x²+y²≤2y Podobnie w pierwszym zadaniu. Przecież z Twojego opisu nie wynika, o który obszar chodzi.

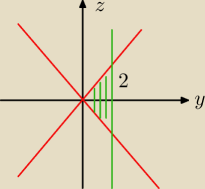
jc: Zrób sobie przekrój płaszczyzną x=0.

jc: Nie musisz nic robić, sam zrobiłem. Spójrz na rysunek.

Michał :): Masakra JC dziękuję Ci za próby wytłumaczenia tego b) bardzo doceniam starania... Ale jakoś nie mogę tego załapać, zapytam pana psora mam jutro laborki/ pon wykład. Może jakoś się dogadamy X_x Ale dzięki a) zrobiłęm wynik się prawie zgadza w sensie... jest zapisany na trochę innych liczbach ale po wykonaniu działan jego wartośc jest podobna ^^ czyli chyba dobrze

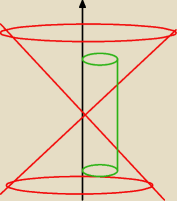
jc: Interesuje nas obszar zielonego walca pomiędzy stożkami. Czy teraz widzisz?