W czworokącie ABCD geo: W czworokącie wypukłym ABCD punkty MN są środkami przekątnych Idpowoednio AC i BD a punkty P i Q środkami boków odpowoednio AB i CD. Udowodnij, że odcinki MN i PQ są prostopadłe wtedy i tylko wtedy gdy BC= AD Wiem że trzeba wykorzystać że iloczym skalarny wektorów MB i PQ to 0 ale nwm jak wyznaczyć PQ (w podr jest że PQ=1/2 (AD+BC))

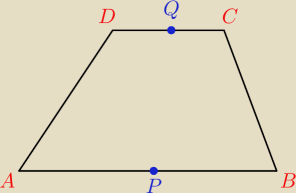
Adamm: Środek ustalam w punkcie A.

	1
Wtedy P =		B
	2

	1
Q = D+		(C−D)
	2

	D+C−B
PQ = Q−P =
	2

Adamm:

	D+B−C
NM =
	2

	1
NM•PQ =		(D+B−C)•(D+C−B)
	4

(D+B−C)•(D+C−B) = (D+BC)•(D−BC) = |D|²−|BC|² = 0 ⇔ |D| = |BC| czyli |AD| = |BC|