geo basted: Nappisać równania stycznych do hiperboli o rownaniu 4x²−y²=4 poprowadzonych z pkt A(1,4)

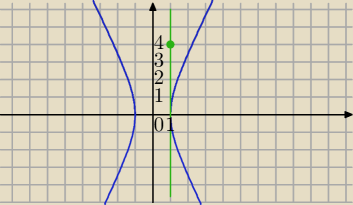
Mila: A=(1,4) nie należy do wykresu hiperboli 1) jedna styczna to x=1 2) Nie znamy punktu styczności P=(x₀,y₀) równanie stycznej do hiperboli: 4x²−y²=4 /:4

	y2
x2−		=1
	4

	y02
(*) s: x*x0−		=1
	4

==================− równanie stycznej w punkcie P=(x₀,y₀) należącym do hiperboli Dla A=(1,4) mamy: x₀−y₀=1⇔x₀−1=y₀ P(x₀,y₀)∊hiperboli to spełnia jej równanie 4x₀²−y₀²=4⇔4x₀²−(x₀−1)²=4⇔ 3x₀²+2x₀−5=0 Δ=64

	−2−8		−2+8
x0=		lub x0=
	6		6

	5
x0=−		lub x=1
	3

	8
y0=−		lub y0=0
	3

	5		8
P1=(−		,−		, P2=(1,0)
	3		3

Równania:

	5		8   −   3
s1: x*(−		)−y*		=1⇔
	3		4

s₁: 5x−2y+3=0 s₂: 1x=1 ==================