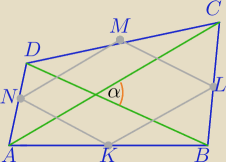
zadanie z geometrii kuba: W trapezoidzie połączono środki boków otrzymując czworokąt KLMN. a) Udowodnij, że czworokąt KLMN jest równoległobokiem. b) Oblicz pole czworokąta KLMN, wiedząc, że przekątne trapezoidu przecinają się pod kątem 30∘, a jego pole jest równe 24cm²

janek191: a) Tw. Talesa

Mila: b) P_ABCD=24 cm²

	1
1) ΔNMD∼ΔACD w skali k=		⇔
	2

	1
PΔNMD=		PΔACD
	4

	1
PΔKBL=		PΔACB
	4

	1
PLMC=		PDBC
	4

	1
PAKN=		PABD
	4

	1		1		1		1
PKLMN=24−(		PΔACD+		PΔACB+		PDBC+		PABD)=
	4		4		4		4

	1
=24−		(24+24)=24−12=12
	4

	1
PKLMN=		PABCD
	2

===================