parabola i okrąg basted: Dana jest parabola P:y²=8x oraz okrąg O:x²+y²=9. Znaleźć równania styznych do paraboli prostej przechodzącej przez punkty przecięcia tych linii

ite: Czy drugie zdanie polecenia jest dobrze przepisane?

basted: "Znaleźć równania stycznych do paraboli prostej przechodzącej przez punkty przecięcia tych linii" Jedyny błąd to napisalem styznych zamiast stycznych ale tak to dobrze

basted: Mi sie wydaje że chodzilo o znalezienie równania prostej przechodzącej przez pkt przecięcia

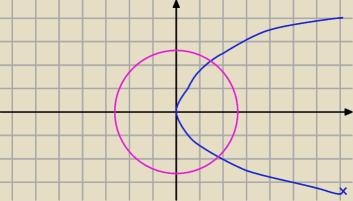
ite: poddaję się, bo nie rozumiem tego polecenia : (

basted: Chyba trzeba znaleźć równanie prostej która przechodzi przez te 2 pkt w ktorych przecina się parabola z okręgiem

basted: A tak wgl to jak się tutaj rysuje takie wykresy

basted: Chyba mam, zrobilem układ równań i wyszły mi 2 pkt przecięcia, A(1,2√2) B(1,−2√2) i prosta będzie pionowa więc równanie prostej przechodzącej przez te pkt bd miała postać: x=1

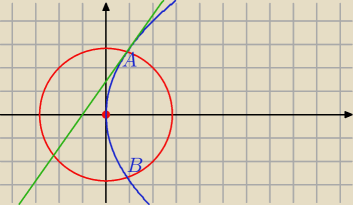
janek191: y² = 8 x x² + y² = 9 więc x = 1 y = 2√2 lub y = − 2√2 Punkty przecięcia krzywych: A = ( 1 , 2√2) B = ( 1 , − 2√2) y = √ 8 x = 2√2 √x

	2 √2
y ' =		= √2x}
	2 √x

a = √2 y = √2 x + b 2 √2 = √2*1 + b ⇒ b = √2 y = √2 x + √2 ============== Dokończ

janek191: Znajdź równanie drugiej prostej stycznej do paraboli w punkcie B.

Satan: basted, mała uwaga. Prosta jest styczna do wykresu funkcji tylko wtedy, gdy ma dokładnie jeden punkt wspólny z ową funkcją. A to znaczy, że prosta x = 1 na pewno nie będzie styczna do funkcji.

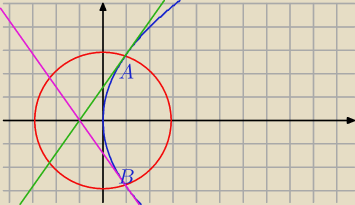
janek191: y = − 2√2 √x y ' = − √²_x a₁ = −√2 y = − √2 x + b −2 √2 = − √2 + b ⇒ b = − √2 y = − √2 x − √2 ===============

Jerzy: 17:57 .... pewnie miałeś na myśli: „ ma jeden punkt wspólny z wykresem funkcji” , ale to nieprawda.

janek191: Pewnie było takie polecenie: Znajdź równania stycznych do paraboli przechodzących przez punkty przecięcia tych linii.

basted: janek, możesz mi napisać co trzeba liczyc od momentu gdzie nam się zgadza czyli tam gdzie jest pkt A i B, chodzi mi abyś trochę wyjaśnił jak obliczyłeś te 2 równania, bo do momentu wyznaczenia A i B to wiem, a na samych wynikach to trochę ciężko

janek191: y² = 8 x ⇒ y = 2√2√ x lub y = −2√2√ x Liczymy pochodną funkcji y ' = √²_x a = y '(1) = √2 − współczynnik kierunkowy stycznej do paraboli w punkcie A y = √2 x + b równanie dowolnej prostej Ma przechodzić przez A, więc 2√2 = √2*1 + b ⇒ b = √2 Równanie prostej stycznej do danej paraboli w punkcie A y = √2 x + √2 ================ Analogicznie dot punkty B