Całka kasia:

	e2x
∫
	1+ex

u=1+e^x du=e^x dx wynik wychodzi 1+e^x − ln|1+e^x|, w odp. jest bez tej jedynki na początku. Wiem, że jeżeli wezmę u=e^x to wyjdzie. Ale dlaczego z tym podstawieniem nie wychodzi?

ABC: co masz na myśli mówiąc nie wychodzi, czy pochodna twojej funkcji jest równa funkcji wyjściowej?

kasia: @ABC, hej! Chodzi mi o to, że jeśli wezmę podstawienie u=e^x to wychodzi taki wynik, jak w odp. Ale nie widzę błędu w moim podstawieniu i nie mam pojęcia dlaczego wychodzi źle.

kasia: Jedynkę mogę potraktować jak stałą, ale przy całkach oznaczonych ona zmieni wynik.

kasia: A nie, nie zmieni! Bo przeciez sie odejmie. XD

ABC: no właśnie

kasia: Jeszcze mam pytanie: czy żeby korzystać z podstawienia Eulera musimy mieć pierwiastek z trójmianu w mianowniku, czy moze byc w liczniku?

ABC: specjalistą od podstawień Eulera jest Mariusz może się potem wypowie , z tego co ja pamiętam normalnie używasz ich do całek typu ∫ √ax²+bx+c dx ale niektórzy nazywają np w całce

	dx
∫		takie podstawienie √x2+c=t−x również podstawieniem Eulera
	√x2+c

kasia: Dziękuję

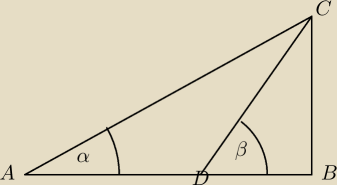
Mariusz: Niech dane będą długości dwóch boków trójkąta ABC (to jakich boków zależy od postaci kanonicznej trójmianu) Niech CD będzie dwusieczną kąta 90−α

	CB
Wyraź		za pomocą danych długości boków trójkąta ABC
	BD

Ja wymyśliłem to zadanie zainspirowany filmikami amerykańców Rozwiązanie tego zadania pozwoli wybrać odpowiednie podstawienie Eulera Podstawienia Eulera wyprowadza się prowadząc sieczną do krzywej y² = ax²+bx+c Podstawień Eulera możesz używać do całek ∫R(x,√ax²+bx+c)dx gdzie R(x,y) to funkcja wymierna dwóch zmiennych Dzięki zastosowaniu jedynki trygonometrycznej możesz ich użyć także do całek postaci ∫R(cos(x),sin(x))dx gdzie R(x,y) to funkcja wymierna dwóch zmiennych