Zasada szufladkowa Paral: Pomoże ktoś rozwiązać i zrozumieć kilka zadań? 1. Każdy punkt okręgu pomalowano na jeden z dwóch kolorów. wykazać, że istnieje trójkąt równoramienny wpisany w ten okrąg o wszystkich trzech wierzchołkach jednego koloru. 2. W kuli o promieniu 1 leży dziewięć punktów. Uzasadnić, że wśród nich można znaleźć dwa odległe o nie więcej niż √3. 3. Spośród wszystkich wierzchołków 17−kąta foremnego wybrano dziesięć. Wykazać, że wśród wybranych punktów są cztery będące wierzchołkami trapezu. 4. Na płaszczyźnie danych jest 17 punktów, z których żadne trzy nie leżą na jednej prostej. Każda para punktów została połączona czerwonym, niebieskim lub zielonym odcinkiem. Udowodnić, że wśród powstałych trójkątów istnieje trójkąt o wszystkich bokach tego samego koloru. 5. W przestrzeni danych jest 6 punktów, z których żadne cztery nie leżą na jednej płaszczyźnie. Łącząc niektóre z tych punktów narysowano 10 odcinków. Wykazać, że w ten sposób uzyskano co najmniej jeden trójkąt.

ABC: Zad 2) Taką kulę możesz pokryć ośmioma sześcianami o boku 1, ponieważ punktów jest 9, istnieje sześcian w którym są przynajmniej dwa punkty, a skoro tak , to odległość między nimi nie przekracza długości przekątnej sześcianu czyli √3

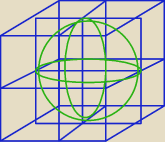
iteRacj@: Chodzi o takie "zamknięcie" jej w ośmiu sześcianach, tak?

ABC: tak

iteRacj@: to już wszystko jasne, dzięki

jc: (1) Wpisz w okrąg pięciokąt foremny. Co najmniej 3 wierzchołki będą tego samego koloru. Utworzą one trójkąt równoramienny.

jc: (3) Zaznaczasz nie wybrany wierzchołek. Pozostałe łączysz 8 odcinkami równoległymi. Na pewno znajdziesz dwa odcinki z wybranymi wszystkimi końcami. Inaczej mielibyśmy co najwyżej 9 wybranych punktów. Końce tych odcinków utworzą trapez.

jc: (4) Wydaje się, że wystarczy 12 punktów. Załóżmy, że taki trójkąt nie istnieje. Weźmy dowolny punkt. Wychodzi z niego 11 odcinków, z których co najmniej 6 jest tego samego koloru (niech to będzie kolor czerwony). Końce tych 6 odcinków mogą być połączone odcinkami koloru niebieskiego lub zielonego. Weźmy dowolny z końców tych 6 odcinków. Wychodzi z niego 5 odcinków w tym co najmniej 3 tego samego koloru ( np. zielonego). 3 końce tych odcinków muszą być połączone odcinkami koloru niebieskiego, a więc mamy trójkąt niebieski. Sprzeczność. A może jest tu jakiś błąd? Nie przypadkowo odcinków miało być 17.

jc: Nie odcinków, tylko punktów.

Paral: co do 5 zadania, mogę skorzystać z twierdzenia Mantela? Mam 6 wierzchołków, czyli maksymalna

	62
liczba krawędzi bez trójkątów wynosi		= 9, a mamy w treści zadania podanych 10
	4

krawędzi, więc w ten sposób uzyskamy co najmniej jeden trójkąt

jc: Tak. Twierdzenie znałem bez nazwy.

jc: Czytałeś coś Parala?