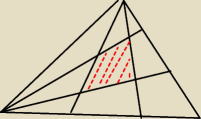
tort Jezrzy: Ania pokroiła tort w kształcie trójkąta 4 cięciami. Cięcia wychodzące z jednego wieszchołka dzielą przeciwległy bok na 3 równe części. Jaką częśc całego tortu stanowi środkowy kawałek? Odpowiedz to 9/70. Proszę o kompletne rozwiązanie

Ania: A nie 1/9 czasem? XD

jc: 9/70 Moje rozwiązanie jest rachunkowe. Prawy wierzchołek = 0, pozostałe: A, B.

	1		1		2		2		4		1
Punkty przecięcia P=		A +		B, Q=		A +		B, R=		A+		B
	4		4		5		5		7		7

(trójkąt = połowa czworokąta).

	9
Wyznacznik ( Q−P, R−P) =		wyznacznik (A, B)
	70

Wkładając odpowiednio dużo wysiłku znajdziesz rozwiązanie rysunkowe, tylko po co?

Jerzy: jc, może być rachunkowe rozwiązanie, niestety z twojego niewiele rozumiem. Co to A,B,P,Q,R...? I skąd teułamki w 2 linijce

Jerzy: Skad np 1/4 przy punktach przeciecia?

jc: 0 to początek świata, A, B wektory (wodzące). Zamiast zera można wziąć dowolne C i wtedy będziesz miał np.

1		1		5
	A +		B +		C (1/4, 1/4, 5/4 to współrzędne barycentryczne).
4		4		4

P, Q, R to 3 wierzchołki środkowego czworokąta.

	1
Jak znalazłem R? R leży na przecięciu odcinka łączącego A z		B
	3

	2
i odcinka łączącego B z		A.
	3

	2		1
R=a		A + (1−a)B = b		B +(1−b)A
	3		3

Stąd

2		1
	a=1−a,		B=1−a, wystarczy rozwiązać układ równań.
3		3

Na koniec korzystam ze wzoru na pole równoległoboku rozpiętego przez 2 wektory.

jc:

	1		1		1
Głupi błąd. Na początku powinno być		A +		B +		C,
	4		4		2

ale u nas C to zero. Reszta o.k.