Zadanie z analizy matematycznej I Studia Funkcje Natalia: Czy funkcja sin(1/x) jest ciągła jednostajnie w przedziale 0<x<1, a funkcja √x w przedziale 0≤x≤∞?

wredulus_pospolitus: nie i nie

Natalia: wredulus_pospolitus dlaczego nie? jak to sprawdzić ?

ABC: jeśli chcesz udowodnić że nie jest jednostajnie ciągła , to musisz pokazać że gdy będziesz "wąskim paskiem jeździć " to i tak funkcja jest tak stroma że ci gdzieś wyskoczy, czekaj może zaraz ci narysuję słabo rysuję tu ale może mi się uda

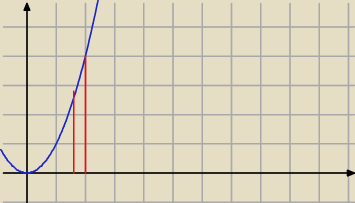
ABC: zobacz funkcja x² nie jest jednostajnie ciągła na <0,+∞) bo jak tym paskiem pójdziesz dalej w prawą stronę to różnica między wartościami funkcji będzie coraz większa

Natalia: ABC dziękuje, rozumiem

wredulus_pospolitus: można też spojrzeć na to w ten sposób: jeżeli wartość pochodnej w punkcie x₀ dąży do ±∞ wtedy funkcja NIE JEST jednostajnie ciągła. dla przykładu:

	1		1
f(x) =		−> f'(x) = −
	x		x2

lim_{x0 −> 0⁺} f'(x₀) = −∞

Adamm: Takie uzasadnienia są dobre − dla małych dzieci. Załóżmy że sin(1/x) jest jednostajnie ciągła na (0, 1). Wtedy dla każdego ε>0 istnieje δ>0 że dla każdych x, y∊(0, 1) mamy |x−y|<δ ⇒ |sin(1/x)−sin(1/y)|<ε np. istnieje delta że |sin(1/x)−sin(1/y)|<1/2 dla |x−y|<δ sin(1/x) = 0 dla x = 1/kπ, k całkowite dodatnie sin(1/y) = 0 dla y = 1/(π/2+2kπ) weźmy takie same k w obu przypadkach, i weźmy je tak małe żeby |x−y|<δ. Jest to możliwe bo 1/kπ oraz 1/(π/2+2kπ) dążą do 0 gdy k dąży do nieskończoności wtedy |sin(1/x)−sin(1/y)| = 1 < 1/2, sprzeczność Zatem sin(1/x) nie jest jednostajnie ciągła

Adamm: Z drugiej strony, √x jest ciągła na [0, 1], a na [1, ∞) ma ograniczoną pochodną ⇒ jest jednostajnie ciągła

ABC: Adamm a ja myślę że intuicje matematyczne dla studentów którzy mają problemy powinny wyprzedzać poprawnie zapisany dowód i też mogę być złośliwy − za dowód który podałeś a w szczególności zdanie "sin(1/y) = 0 dla y = 1/(π/2+2kπ)" dostałbyś ode mnie ocenę 2+ε

jc: E tam. To literówka.

ABC: fakt jest taki że człowiek który uważa innych za małe dzieci nie zapisał poprawnie dowodu dobra kończę bo cenzura zaraz to wytnie i tak

Mariusz: W dodatku dla f(x) = √x , 0≤x≤∞ korzysta z pomysłu którego wcześniej uznał że jest "dla małych dzieci" ABC spojrzałem do Fichtenholza i ma on tam przedstawiony podobny rysunek

Mariusz: ABC między wami jest różnica pokolenia + to że wyżebrał od Jakuba możliwość usuwania wpisów powoduje że pozwala sobie na takie wpisy

Adamm: @Mariusz 1. Pisałem to zanim zobaczyłem post 18:28 ale i tak powątpiewam w prawdziwość tego co napisał wredulus generalnie to jego wpisy zazwyczaj są fifty−fifty, szczególnie te teoretyczne a to co było na górze, to było uzasadnienie typu "to widać" 2. Nie mam możliwości usuwania wpisów. Może po prostu byłeś bardzo chamski i ktoś uznał że usunie twój post? Nigdy o tym nie pomyślałeś? 3. Co do tego ma różnica pokolenia, jeśli jedyne co robisz to widzisz wszystko w negatywnym świetle, nie mogąc wyjść z dołka?

Adamm: a po 4, to żałosny jest fakt że wasze dumy sięgają szczytów obraziłem cię ABC? Nie, wygarnąłem metodę.

Mariusz: Od razu domyśliłem się że ten wpis ABC był spowodowany tym komentarzem o " małych dzieciach " Gdyby postawił ci dwóję za ten wpis to zachowałby się jak ten szczeniak ledwo po studiach co miał ze mną matematykę w podstawówce Wpis Adama jest o tyle cenny że przedstawia sposób postępowania nawet jeśli znajdują się w nim drobne błędy Z tą różnicą pokolenia to miałem na myśli to że w podobny sposób piszą młodzi ludzie którym od nadmiaru uprawnień przewróciło się w głowie Wspomniałem o książce Fichtenholza Trochę o ciągłości jednostajnej jest w Tom 1 §5 punkt 86. Zadanie podobne do pierwszego tylko z innym przedziałem podane jest u Fichtenholza jako przykład Punkt 87. to twierdzenie związane z ciągłością jednostajną Ma ono postać implikacji więc jest mało przydatne Jeżeli funkcja jest określona i ciągła na przedziale domkniętym to jest na tym przedziale jednostajnie ciągła

jc: Mariusz, przedział domknięty możesz zastąpić zwartym podzbiorem przestrzeni metrycznej.