Geometria analityczna ......: Trójkąt ABC jest rownoramienny w którym |AC|=|BC|. podstawa AB zawiera się w prostej k: 3x−7y+35=0, zaś ramie BC zawiera się w prostej l: 5x−2y−19=0. Wyznacz równanie prostej, w której zawiera się bok AC tego trójkąta jeśli wiadomo, że punkt P(−2,0) należy do boku AC

6latek: najpierw zrob rysunek

......: A co dalej?

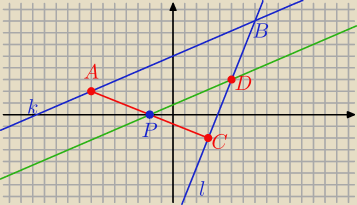
janek191: B = ( 7, 8) D = ( 5, 3) → BD = [ − 2, − 5] I BD I = √4 + 25 = √29 A = ( x, y) P = ( − 2, 0) → AP = [ − 2 − x, − y ] I AP I = √ 4 + 4 x + x² + y² więc x² + 4 x + 4 + y² = 29

	9		30
x2 + 4 x + 4 +		x2+		x + 25 = 29 / * 49
	49		7

49 x² + 196 x + 9 x² + 210 x = 0 58 x² + 406 x = 0 x² + 7 x = 0 x*( x + 7) = 0 x = − 7 y = 2 A= ( − 7, 2) itd. C = ( 3, − 2)

janek191: I sposób rozwiązania: 1) Wyznaczamy punkt B 2) Wyznaczamy prostą PD II k oraz punkt D 3) Obliczamy długość odcinka BD, I BD I = √29 4) Na prostej k wyznaczamy punkt A = ( x, y) odległy od punktu P o √29 5) Wyznaczamy prostą AP oraz punkt C. Patrz: 15 V 23.16 II sposób: 1) Wyznaczamy punkt B 2) Wyznaczamy prostą PD II k oraz punkt D 3) Wyznaczamy środek odcinka PD oraz prostą prostopadłą do prostej k przechodzącą przez wyznaczony punkt 4) Wyznaczamy punkt C − punkt wspólny tej prostej z prostą l 5) Wyznaczamy prostą PC czyli AC.